Ex 2.24

The interpreter expression is easy to generate. As a box-and-pointer diagram, here’s what it is:

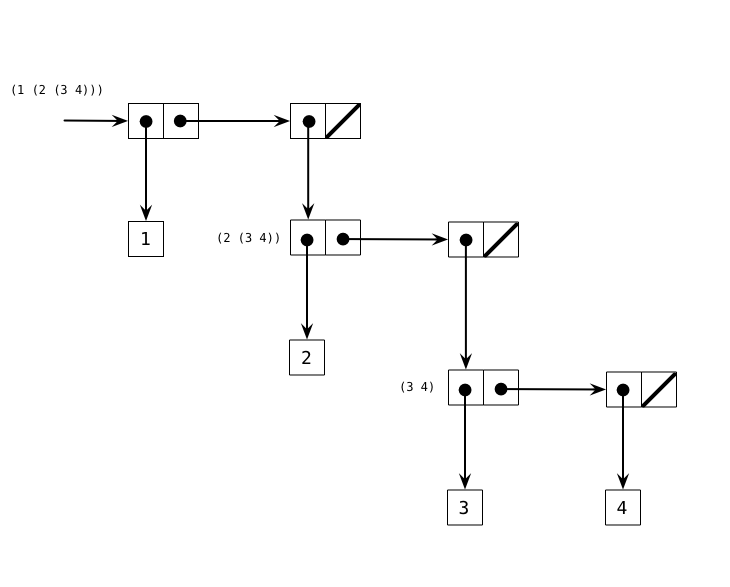
One quick check that can be done using a box-and-pointer diagrams is to count the number of lists. We know from the expression that, with three parenthesized statements, three lists must be present. On a box-and-pointer diagram, a list will be a horizontal sequence of boxes, terminating in a ‘null’ slashed box. We see that much, so we aren’t far off. The additional labels on each list are also helpful to double-check each sub-section of the list (while the text shows such labels with pointer arrows, I’d rather only have one on the very first label, since the other references don’t exist as such in the expression statement.)

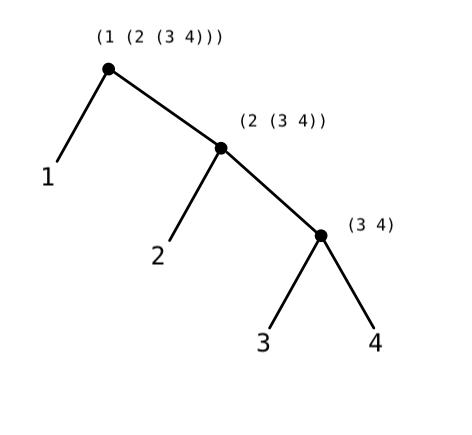
The tree representation is certainly simpler, but isn’t that much different than the box-and-pointer. There are just some details removed. It’s less explicit about the underlying data structure, so it’s not as if the box-and-pointer diagrams have no place.

Ex 2.25

This exercise doesn’t have much to it, once you’ve already solved it. Hopefully using the testing function made it easier to find out what was right and what was wrong. One thing to point out is that any expression to find a (numeric or similar) value necessarily begins with car, because cdr will always return a list.

Ex 2.26

Again, not much to talk about here. If any of these are difficult to follow, putting together the box-and-pointer diagrams may help to develop an understanding of the difference between lists and pairs.

Ex 2.27

It’s not hard to build this on the pattern of the original reverse from 2.18. There simply needs to be an extra condition to check if the current item being ‘moved’ is itself a list. In that case, we recursively run deep-reverse on that list. In my procedure, I used the list? predicate, which I don’t think is mentioned in the text, but is quite useful here. For the tests I put in, pair? would also work, although passing in an actual non-list pair might result in errors.

Ex 2.28

This is similar to the previous problem. We’re still looking for list elements within lists and going into them (a ‘deep’ procedure), so it has the same conditional structure as deep-reverse. The difference is in how the result is formed. This time I went with append to join sub-lists together, ensuring that the left-to-right order is preserved. In the last statement of the condition, where the final fringe values are found, they need to be wrapped in a list. That way the procedure above them doesn’t need to care whether it operated on a fringe element or a section of the tree.

Ex 2.29

Now we’re applying the techniques we’ve used so far to working with data structures. In part a, we need to pull out the right element from a list using car and cdr, as in 2.25. Parts b and c are both procedures that traverse the structure, in much the same way as 2.27 and 2.28.

I’ll compare how I did this one to my solution for fringe in the previous exercise.

(define (branch-weight br)
  (if (is-mobile? (branch-structure br))
      (total-weight (branch-structure br))
      (branch-structure br)
      )
  )

(define (total-weight mob)
  (+ (branch-weight (left-branch mob)) (branch-weight (right-branch mob)))
  )
  
; Fringe (for comparison)

(define (fringe li)
    (cond
      ((null? li) null)
      ((pair? li) (append (fringe (car li)) (fringe (cdr li))))
      (else (list li))
    )
  )

I created total-weight in such a way as to make use of another procedure, branch-weight. Using this procedure and the selectors for the mobile structure allows total-weight to be written very simply: it is the sum of the branch-weight of the left branch and the branch-weight of the right branch.

Taking the two mutually recursive routines together, the procedure is still quite similar to fringe. We test to see if we’re at an endpoint of the structure or if we’re at a node that can go ‘deeper’. If it’s an endpoint, we get its value (using list in fringe and branch-structure in branch-weight), and if not, we recurse until complete. Fringe also deals with trees of indeterminate ‘width’ and so needs to check for the end of the list; total-weight does not need this as a mobile can only have a left or right branch.

Part c ends up using branch-weight as well, in determining the moment for a particular branch. That again allows the heart of the balanced? predicate to be one expression, using an internally defined moment procedure:

(and (balanced? (left-branch mob))
     (balanced? (right-branch mob))
     (= (moment (left-branch mob)) (moment (right-branch mob)))
)

The mobile is balanced if the left branch and right branch are both balanced, and the moment from the left branch is equal to the moment from the right branch. That’s nearly the same as the exercise’s description of what a balanced mobile is (other than that I called it ‘moment’ instead of ‘torque’).

In case it isn’t clear at this point, using recursive data structures (like most trees, where each node is effectively a tree itself) naturally gives rise to recursive procedures for working with them. They often end up being at least superficially similar to each other in several aspects.

In part d the constructors are changed, and we need to see what else has to change around them. Ideally, only the selectors would need changing, as that is the point of having them in the first place. My additional predicates is-mobile? and is-branch? end up changing too; if you’ve created the other procedures in such a way that they don’t ‘know’ about the internal mobile structure and interact using only constructors and selectors, they ought to remain unchanged as well.

Ex 2.30

The first way to define square-tree is the by-now-familiar method of a cond statement testing whether we’re at an ‘internal node’ of the tree or a ‘leaf [node]’. In the former case, we recurse (constructing the new tree from subtrees), and in the latter we process it.

When using map, some of the same structure can be seen. The test that we pass to map is the same – figure out if this node is internal or a leaf, and process accordingly. With map, we don’t need to bother with constructing the output tree, or checking when we’ve finished, as those are handled automatically.

Ex 2.31

Creating tree-map after making square-tree with a map is quite easy. Just look through square-map for all the times we call square (or sqr in the case of Racket), and replace them with a named argument. If square is passed as that argument, then the result will be the same. The only other thing is to have the arguments to tree-map in the right order, so that they match the procedure’s ‘signature’ given in the text.

Ex 2.32

As the routine suggests, rest is the set of subsets of the ‘rest’ of the list, that is, the cdr. Assuming we have all of those properly created, then we can create all subsets that include the element at the head of the list (in other words, the car of s) by adding the head to each member of rest. We can do that by creating a new set (i.e. list) using cons and our head element. Our routine to pass to map is lambda(x) (cons (car s) x).

It’s important in this case that the null set (empty list) be used as the base to add elements to, otherwise we could not build up the subsets from individual elements. Once we’ve created our new set that includes an element, it is appended to our current group, and that becomes the new rest as we move up the list (backing out of calls to subsets in the let statement).

For illustration, the rest set would develop as shown below for the list (1 2 3). The vertical bar is used as a marker to distinguish the newly added subsets from the ‘old’ set.

()   ; base
; Head is now 3, add that to each set
() | (3) 
; Head is now 2, add that to each set
() (3) | (2) (2 3)
; Head is now 1, add that to each set
() (3) (2) (2 3) | (1) (1 3) (1 2) (1 2 3)

Solutions 2.2.2