Ex. 3.12

First, let’s consider what happens with the constructor version append. It doesn’t change its argument, so x will thus remain unchanged from when it was created. Since x is a list of the symbols a and b, the remainder of the list after the car is just the list (b).

Here’s the box-and-pointer diagrams for x and y when they are first created:

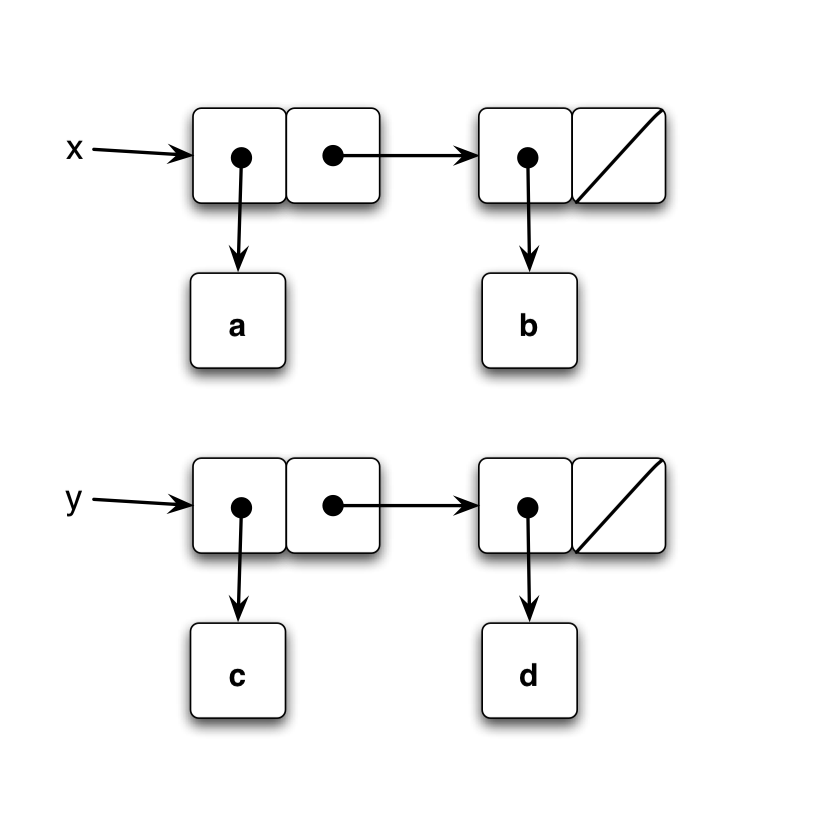
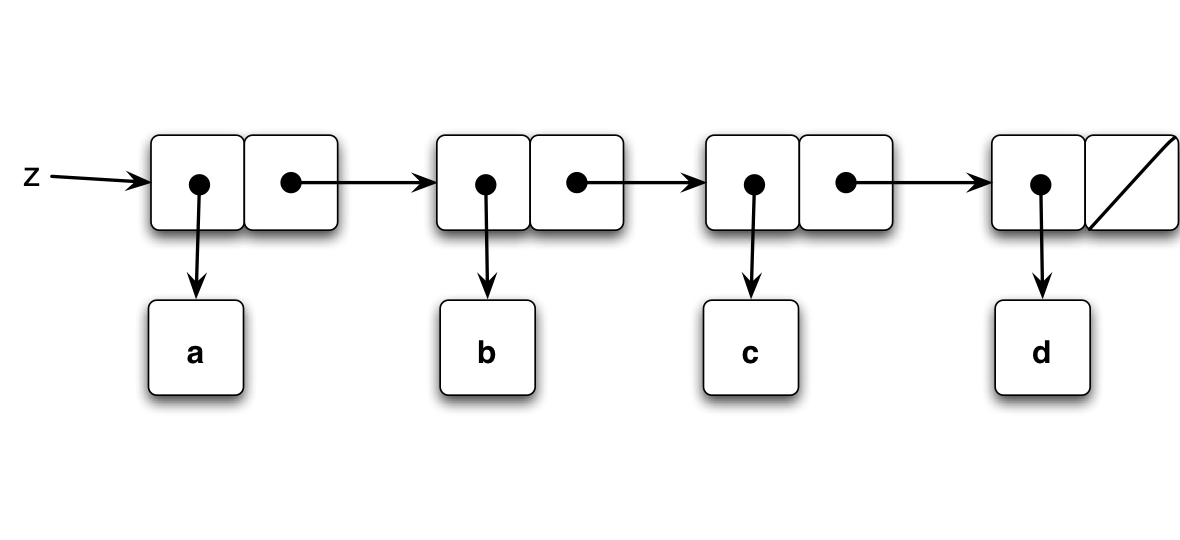
When z is built, it forms a new list that appends y onto x, and it’s a separate list of the same symbols.

Using the mutator form append!, however, can result in changes to the list being appended to. The result w is a list that takes the actual list x points to, and then takes the actual list y points to and attaches it. That means that both w and x end up pointing to the same object in memory (part of which is also pointed to by y). When we ask for the cdr of x after processing it through append!, it now has y at the end. The cdr will not have just one element, but the rest of the original x followed by the entirety of y; in other words, (b c d). Here’s what the box-and-pointer structure looks like:

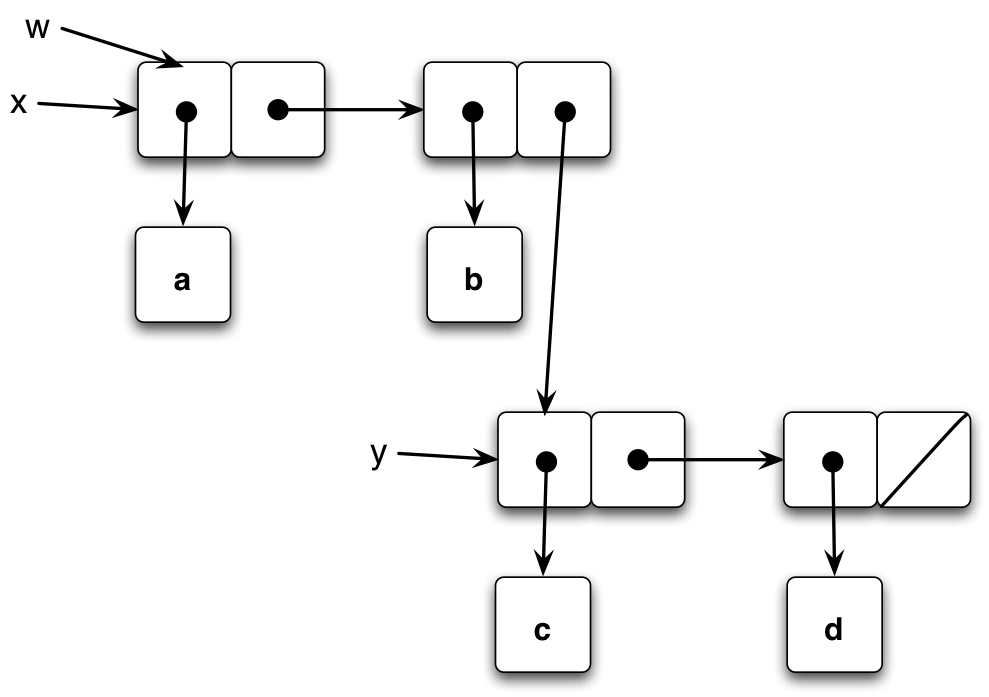
The notable thing about using append! is that it doesn’t take up any extra space, but it does change what the x meant earlier in the program. There’s a tradeoff here that isn’t just about saving space, though. There are indeed times when it’s desirable to have access to the exact thing that is referred to somewhere else. As an example, after the solutions file is finished, w is still defined as it was here, but x has been assigned a new value. If we for some reason wanted to again modify what x originally pointed to, we could still do it using w since it ‘saves’ the reference to the original list.

Ex. 3.13

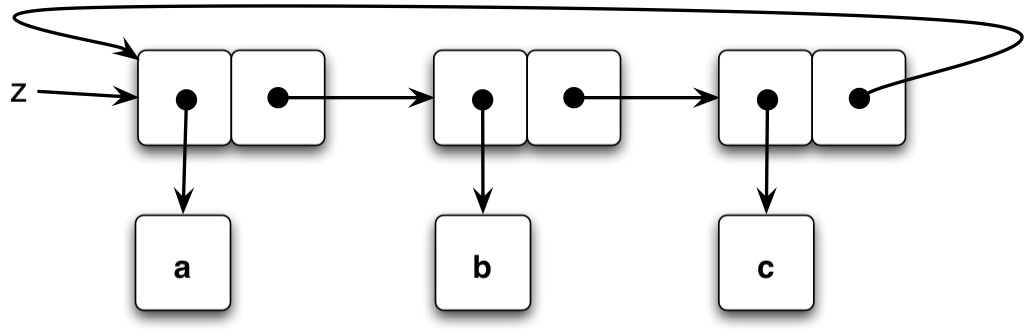
The make-cycle procedure does what it suggests; it takes a list and then makes the end of it point back to the start, removing any terminator from the list. How does it do this? First, it uses last-pair to find the final pair in the list. Recall that the pairs in a list are pointers: One (the car) points to the value stored at that point in the list, and the other (cdr) points to the next pair of pointers in the list, or null if it is at the end of the list. When make-cycle is run, the last pair found will initially have a null pointer as its cdr. When the cdr of that pair is set back to the list itself, that means when the previous last pair is reached, the ‘remainder’ will be the start of the list again.

This is the box-and-pointer diagram that results:

To understand what happens when we call last-pair on a cycle, we have to see how it determines what the last pair in the list is. Let’s look at the procedure again to understand how it functions.

(define (last-pair x)
  (if (null? (cdr x))
      x
      (last-pair (cdr x))
      )
  )

The procedure is recursive, and works by searching for the pair whose cdr is null. In a properly-formed list, this will be the final element of the list. By mutating the list with make-cycle, however, we’ve replaced the last pointer with a pointer to the start of the list. There is no more null pointer to be found, and the procedure does not terminate. Instead, it just keeps continuously checking the cdr of all the pairs in the cycle, and loops forever.

Ex. 3.14

Here’s the code for the mystery procedure, for reference.

(define (mystery x)
  (define (loop x y)
    (if (null? x)
        y
        (let ((temp (cdr x))) 
          (set-cdr! x y)
          (loop temp x)
          )
        )
    )
  (loop x '())
  )

Just looking briefly at what it does, we can see that every iteration of loop gives us a new temp variable and a mutated x. Whatever y starts as will be appended to the first element of x, and this will be the argument y in the next loop. What had previously been the remainder (cdr) of x will be the new x in the following iteration. This will continue until x is empty, and y is returned. The end result is that y is built from successive elements of the initial x, and they are put into the list in reverse order (since y is attached to the end). The procedure is essentially a ‘destructive reverse’ in constant space; the result is a reversed list but the original list has been mutated.

Here’s the analysis using box-and-pointer diagrams. The initial list v is just an ordinary sequence of four pairs:

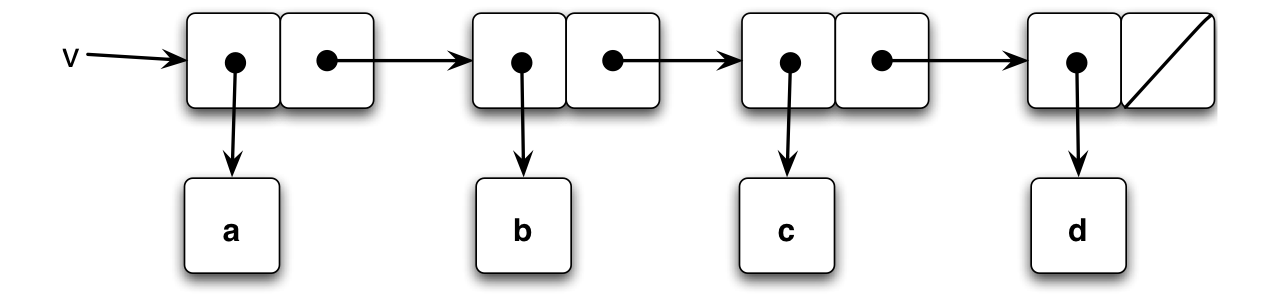
When mystery is run, loop is initially called with x set to the list v points to, and y as an empty list. After the set-cdr! step, the first pair of pointers has been changed. The cdr of x (also v) is set to the empty list, which means it is now a null pointer. It becomes a list with one element, and temp points to the former cdr of the list:

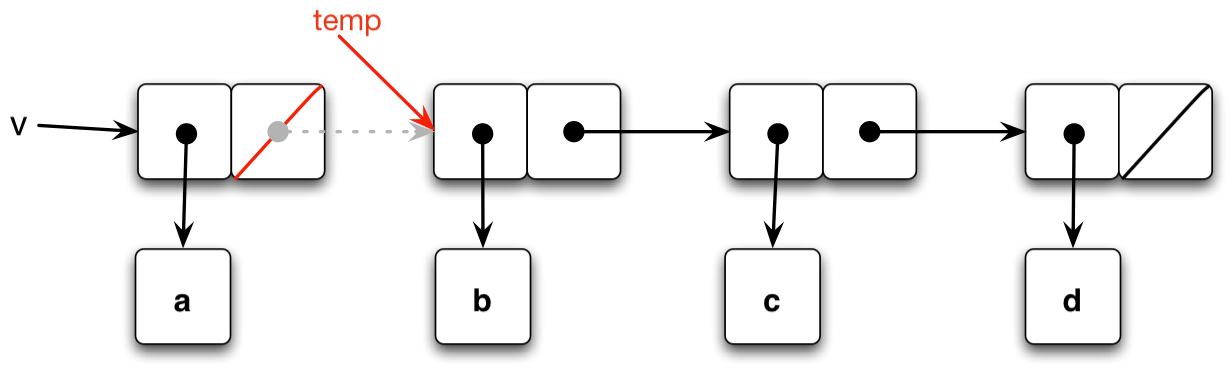
On the next iteration, the first pair of that list will be cut off, and the one-element list that v now points to will be its new cdr, as that was passed as y on the second loop. In the end, the result w is a list that is the original in reverse order. Note that v still exists, but after being changed once, it doesn’t get changed again, so it still just points to a one-element list.

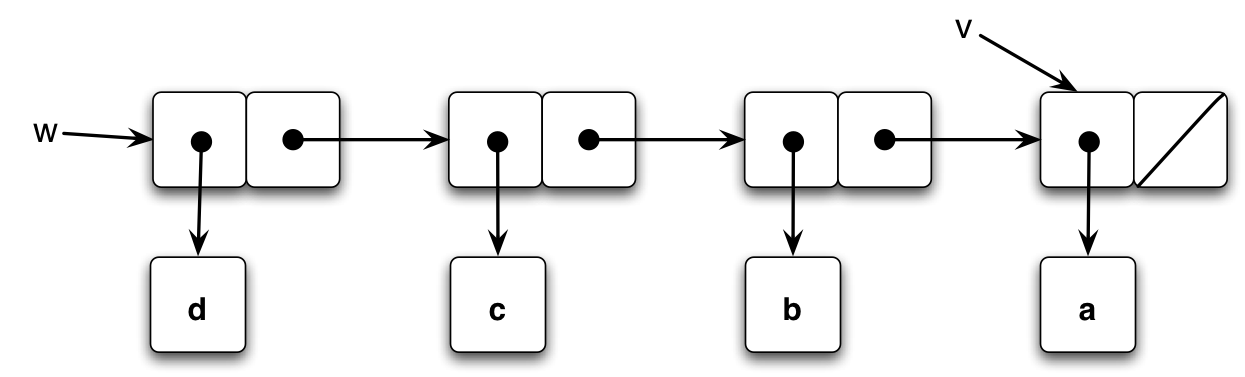
As for what gets printed out for each of the variables, it’s fairly easy to tell based on the box-and-pointer diagrams. For w, it should be the original v, reversed: (d c b a) . For v, just the single-element list (a). This is verifiable with the interpreter.

Ex. 3.15

We already have the results here, and we just need to explain them. The following diagrams will show what is changed. To compare with the original box-and-pointer structure, refer to the figures in the text.

When set-to-wow! is called on z1, it gets the car of z1, and then the car of that, and sets it to 'wow (the symbol). The car of z1 is x (as defined in the global environment), and thus car of x is changed. However, since the cdr of z1 is a pointer to x, the cdr is changed too. Note that when we print z1, it comes out as a list with (the contents of) x as the first element, since the car is actually a pointer to a list.

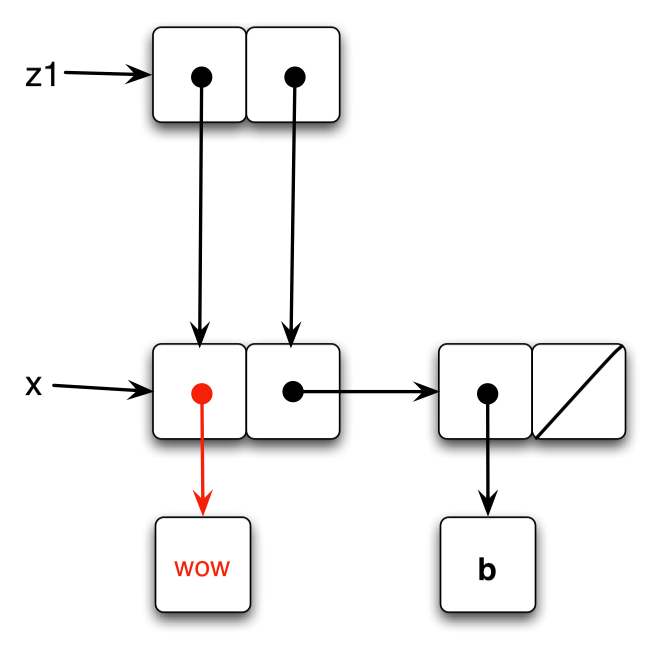
For z2, however, the list pointed to by its cdr is distinct. When set-to-wow! modifies the car of z2’s car, it has no effect on the remainder of z2. The output remains in list form, in the same way z1 was.

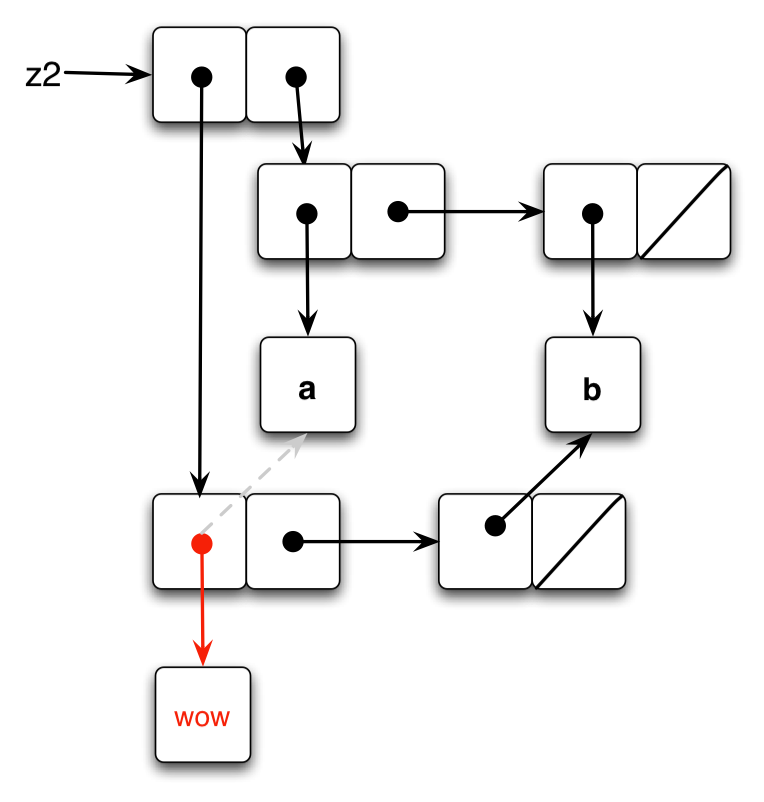
Something to notice here is that set-car! and set-cdr! do not change the actual values pointed to by the pair; what they change is the pointers themselves.

Ex. 3.16

For each of these, it’s almost easier to draw the diagram first, and then figure out how to construct the list afterward in the interpreter. These go from the fairly basic to the more complex.

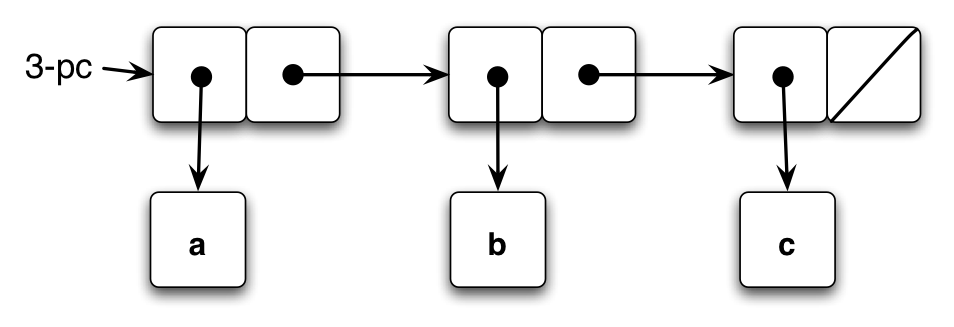
First off, we have three pairs that will be counted as three pairs. This is just a simple list. The count is 1 in the car, and 2 more in the cdr.

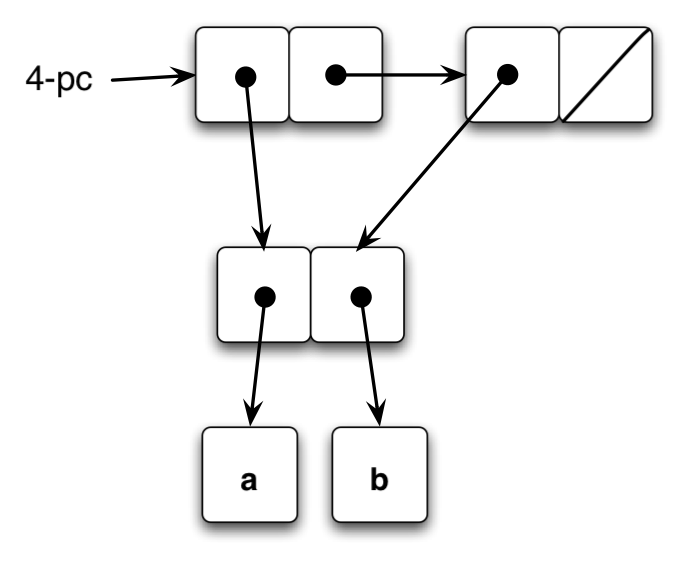
To get a count of four, we will need to count one of the pairs twice. That can be done with a list where the first and second element point to a third pair. The count will be 2 in the car, and 2 in the cdr. It’s the same structure as z1 in the previous exercise.

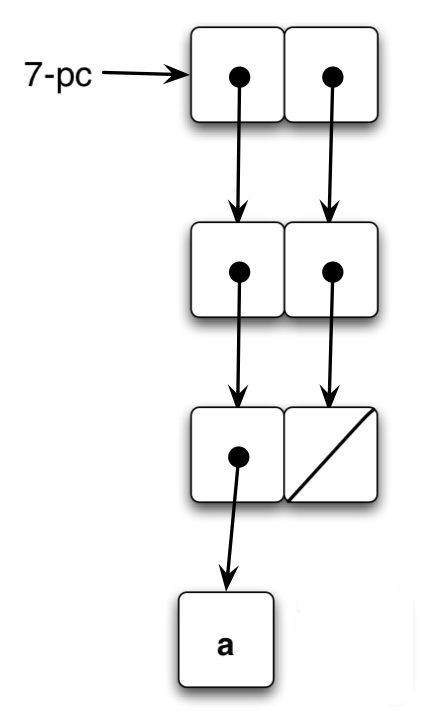
To make it to seven, we need to count two pairs three times, and one pair once. To get that, we create a pair with the car and cdr pointing to a one-element list, and then another pair with the first and second elements both pointing to the other ‘doubled’ pair. It isn’t entirely necessary to make the ‘bottom’ element a list (a simple pair will do), although the exercise did suggest making ‘list structures’ so that is what I’ve done.

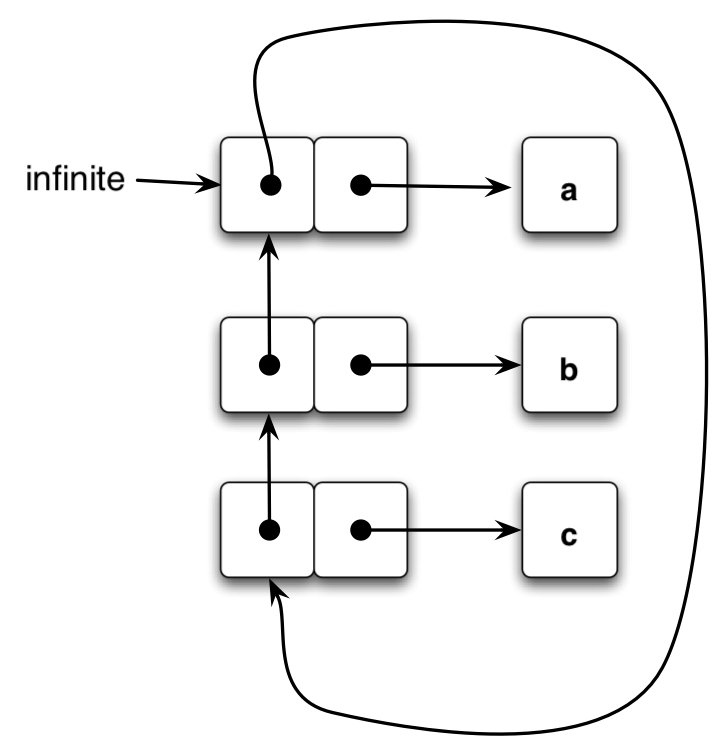
Finally, we want to have a structure that will never return a value. Since we know that the faulty count-pairs will keep looking through the car and cdr until it finds something that isn’t a pair, we need to make sure that at least one of those will always point to another pair. From Exercise 3.13, a structure created with make-cycle will always have another pair to count. We can either make our own cycle using that procedure (from a three-element list) or perform the same steps ourselves. (Note that this particular diagram illustrates loops on the cars, not the cdrs, and this is not producible from make-cycle. It still satisfies the conditions and could be created manually using set-car! on a set of pairs).

Ex. 3.17

The primary problem with the previous version is that some pairs were being counted more than once. We have to avoid that, and that means we need to be able to recognize a pair that’s already been counted. As the hint suggests, we’ll need some additional data structure to keep track of them.

What we can do is make a list of all the pairs already encountered. We then traverse the structure as before, but this time, we check to see if the pair under inspection is already on the list. If it is, then we skip counting it and terminate the search in this direction. If it isn’t, we add it to the list of pairs we’ve encountered, and proceed to check the members of that pair.

To encapsulate the list that tracks the encountered pairs with our procedure, we use a let statement to create the list, and have the traversal procedure as an internal definition. My version of the routine also takes advantage of the fact that the number of pairs logged in the list will actually be the desired result, and so instead of recursively forming a count, it just traverses all pairs and then counts the result at the end. This approach saves storing one variable at the expense of some extra time to read the final count. As it is, the extra time of checking the list on each traversal step is a far bigger expense anyway.

Ex. 3.18

It turns out that finding a cycle can be solved by a process very similar to counting pairs in the last exercise. There are differences, though. For one, we are only looking for a true/false result, so the procedure can exit immediately when it finds the answer. Additionally, we are only considering lists and only checking the cdr of each.

(define (is-cycle? li)
  (let ((cdrs-found '()))
    (define (add-to-found p)
      (set! cdrs-found (cons p cdrs-found))
      )

The start of the procedure is almost identical to that for the corrected pair counter, aside from the names. The internal traversal is where we can see changes.

    
    (define (run-list lis)
      (cond 
        ((null? lis) #f )
        ((memq (cdr lis) cdrs-found) #t )
        (else
         (add-to-found lis)
         (run-list (cdr lis))
         )
        )
      )
    (run-list li)
    )
  )

Since we’re dealing with lists, we check for termination against the empty list. We then go on to see if we’ve encountered this list before. The procedure returns immediately if we find a match for one we’ve already seen, since that means there is a cycle. The last steps are adding the list we checked to the lists found, and then continuing on to the cdr.

Both this exercise and the previous one highlight the nature of pairs (and lists) as being referenced through pointers. Each time, when we added one of them to our tracking list, what we really added was a pointer. We didn’t take the pair itself out of its structure and put it on another list. Importantly, we didn’t put a copy of the pair there either — if we’d done that, it wouldn’t be recognized as the same thing when we check it. How that check is defined is important as well, of course. In both procedures I used memq to verify the values, which relies on the eq? procedure. As discussed in the text, this is true when the two items are the ‘same thing’ in memory; if comparing pointers, they both point to the same actual item.

Ex. 3.19

It’s apparent that finding cycles using the approach above might require storing each item in the list up to the point that a cycle is found. That means for any list we check, we need to have extra space for at least as many pointers as the list itself contains. This could get out of hand for large data structures. A constant space approach is going to be invaluable, if we can discover one.

We need some way to figure out if we’re encountering an ‘already-seen’ item without actually storing the items we’ve already seen. How can we get around the storage problem? Now, it’s not that we can’t add any new storage, it’s just that we can’t let it grow according to the size of the list. We can at least keep track of one item. Suppose we save just one item from the list. If we keep checking forward from there, and there is a cycle, we’ll come back around to that item at some point, at which point we’ll know we’ve found the cycle.

For my initial approach I did this by just storing the first element encountered, but that doesn’t quite cover all cases. A cycle doesn’t necessarily have to comprise the whole list. Imagine a list structure where part of the list loops back, but not to the start of the list (one of the test cases has precisely that). If we expected the cycle to come back to the first item, we’d never see it again, and also never see a null at the end of the list.

To solve that problem, we need to go beyond just checking against a single element, but do have to limit how far we check. While we can’t record all the list elements we’ve found, we can keep track of how many we have checked. However long the cycle is, we’ll eventually have counted enough pairs that a cycle including that element could not be longer than the current number we have already checked. In my solution, every time I check against an entry for a cycle, I increment the forward-count limit. This adds a fair amount of forward checking, but it does only add two additional variables, and thus no dependency on the list length for the space required.

There is a more well-known and fairly efficient solution to this problem, which I imagine is the ‘clever idea’ alluded to in the text. I only learned about it after seeing it mentioned in relation to another topic. It is Floyd’s Cycle-counting algorithm, also known as the ‘Tortoise and Hare’ approach. All that’s needed is two distinct pointers. Each time the ‘tortoise’ pointer advances one step, the ‘hare’ moves ahead two (or more) steps. When there is a cycle, the two pointers must at some point land on the same place. This has the advantage of exiting quickly in the non-cycle cases, as the ‘hare’ pointer reaches the end of the list sooner.

Note that the ‘testing’ done in the file does not actually verify that a constant-space approach was used. It is only able to check if the cycle-counting is still functioning properly. While it may be possible to develop an automated test that can figure out how much space a procedure is using, that’s a subject that is beyond the level of this book. It’s also likely to be not just interpreter-dependent but potentially OS- or processor-dependent as well.

Ex. 3.20

This ends up giving a result no different than with ‘regular’ pairs, but the underlying machinery is relatively complex. We’ll proceed through it one line at a time. I won’t show the structural details of the pair procedures like car and cons; it’s more useful to see what is produced from them. This exercise is somewhat difficult to talk about, as the variables are (almost certainly intentionally) confusingly named. I’ll try to use the environment labels to distinguish them as required.

Firstly, we have a basic variable definition.

(define x (cons 1 2))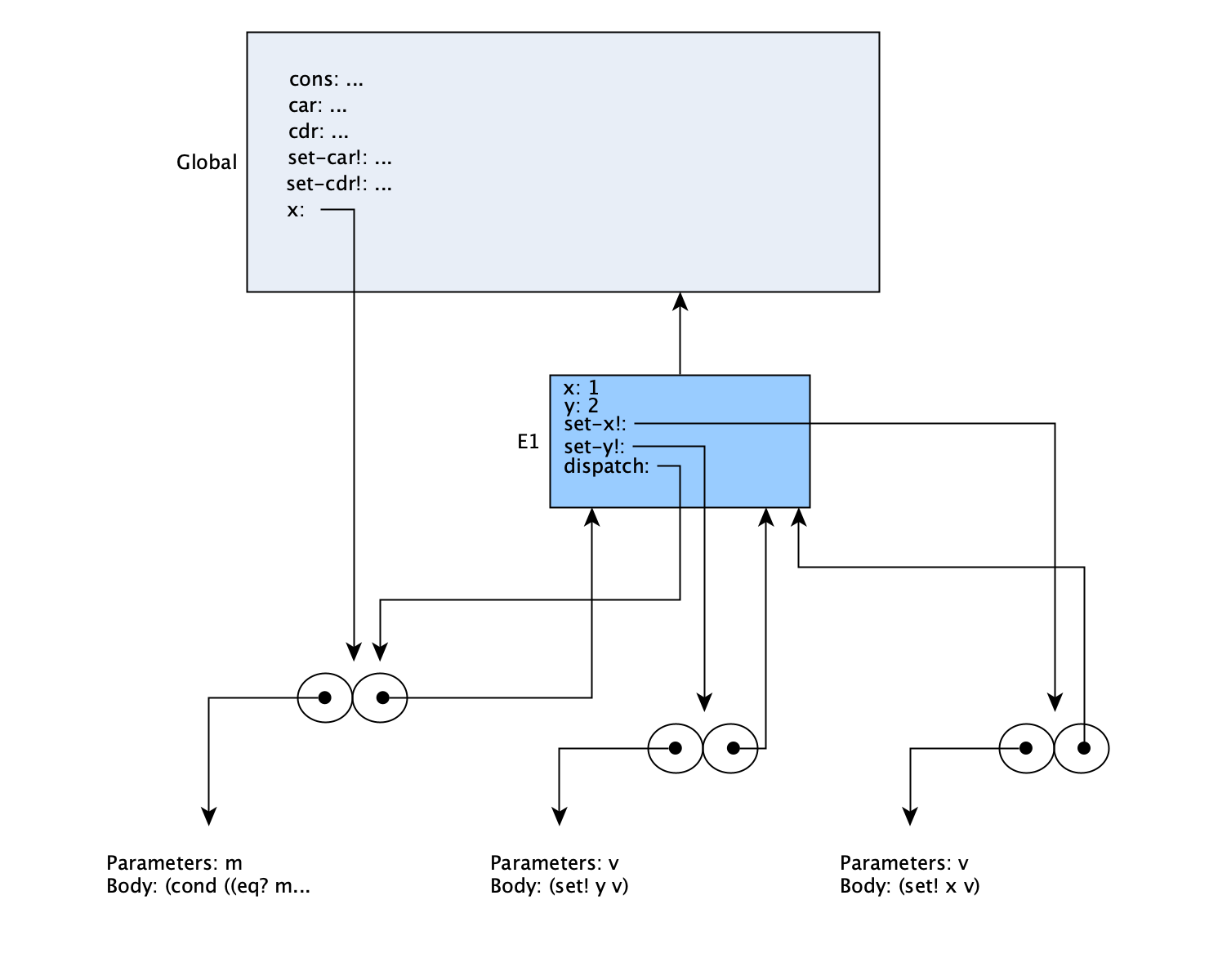

When cons is called, a set of internal procedures will be defined in its execution frame (the frame pointed to by E1 here). When cons is done, it returns dispatch, which is what x is set to in the global environment. The values of x and y in the cons call are saved in the environment E1, and will only be accessible by interactions with that dispatch procedure.

(define z (cons x x))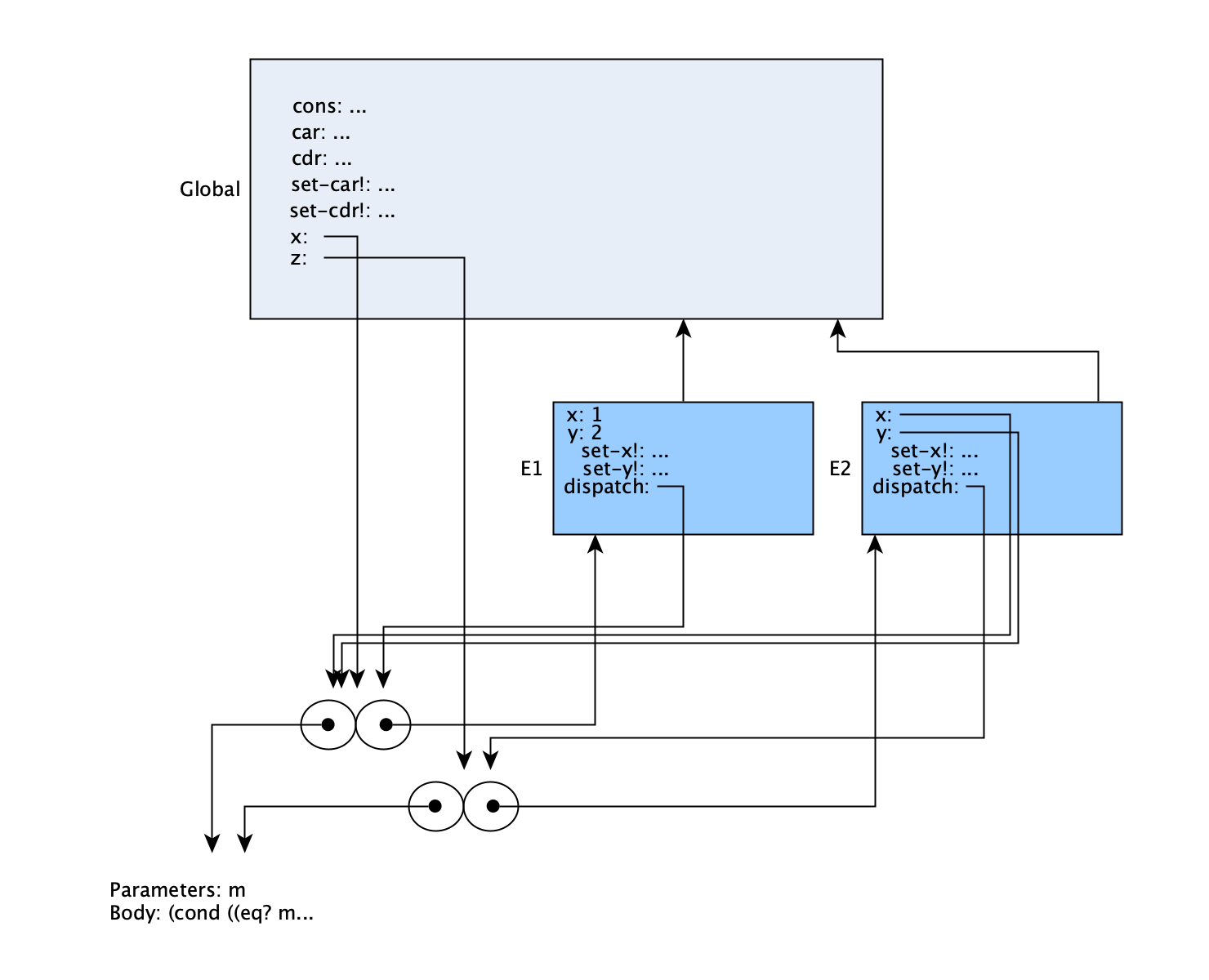

The second call creates another set of procedures, and again returns dispatch, to be set to the global variable z. Since this was called with global x as both of its arguments, we see that in E2, both x and y point to the same procedure object that (global) x does.

While it’s not fully shown, it’s worth pointing out that all of the internally defined procedures in a call to cons are distinct between calls. Only dispatch is diagrammed, but it’s the same pattern for the values of set-x! and set-y! in E1 and E2. Each points to a distinct procedure object. What is indeed shared between the two versions is the code used for the bodies of the procedures.

(set-car! (cdr z) 17)

This line is complex enough that it needs two diagrams. In order to evaluate set-car!, the arguments to it must be evaluated. Technically our model doesn’t define how or when arguments are evaluated, only that there is a ‘binding’ of them. For this reason, the first diagram below doesn’t show the set-car! call; it’s only considering the evaluation of the first argument. However, it will be assumed in the second diagram below that this argument evaluation and binding does happen first, to make it easier to portray.

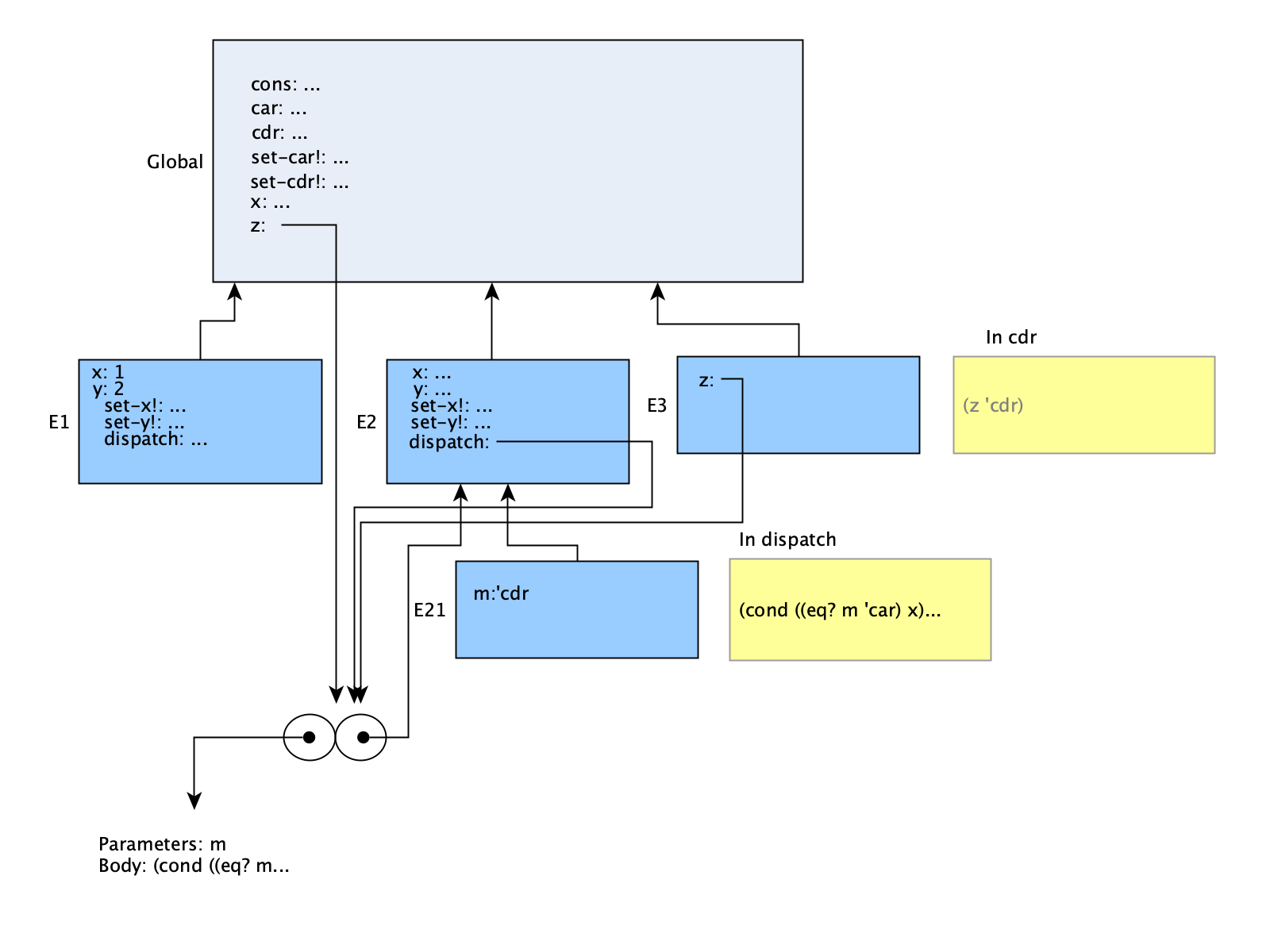
The first argument is a procedure call, and evaluating (cdr z) will require a new environment (E3). In that environment the variable z happens to be the same as global z. Since cdr just has one line, the procedure that E3’s z points to is executed, and is passed the argument of 'cdr (that’s quoted, so it’s the symbol cdr, not the procedure). That will then cause another evaluation frame to be made for dispatch (E21), and it will look for what to do when called with 'cdr. It returns the value of y from E21, which (by looking back into the previous frame E2) is equal to the procedure that global x points to. The second argument to set-car! is just 17, which evaluates to itself (and is not shown in this diagram).

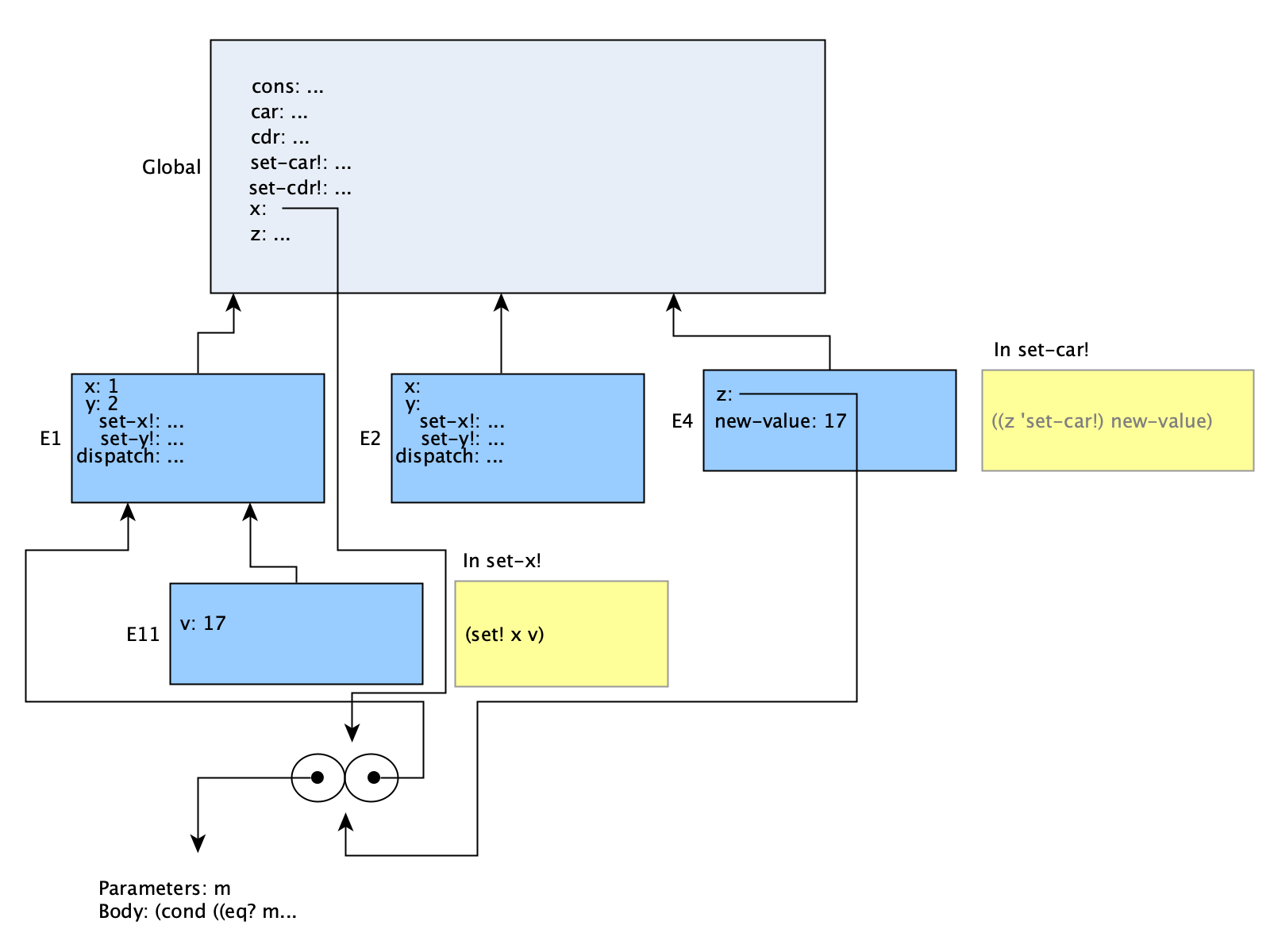
Here we see the call to set-car! with the arguments evaluated and assigned to local names, in E4. The variable z in E4 is pointing to the same thing as global x. The set-car! procedure calls its argument with the symbol 'set-car!, so then “global x” will be called with its version of set-car! and the argument 17 (taken from E4’s new-value). That leads to a call of the set-x! which is defined in E1. This requires a new evaluation frame, shown by environment E11. The procedure will set x in its environment to the new value, 17. Since the frame E11 does not have x defined, it looks back through its frame stack, going first to E1. E1 does have x defined (as 1), and that is the variable that will be changed to 17.

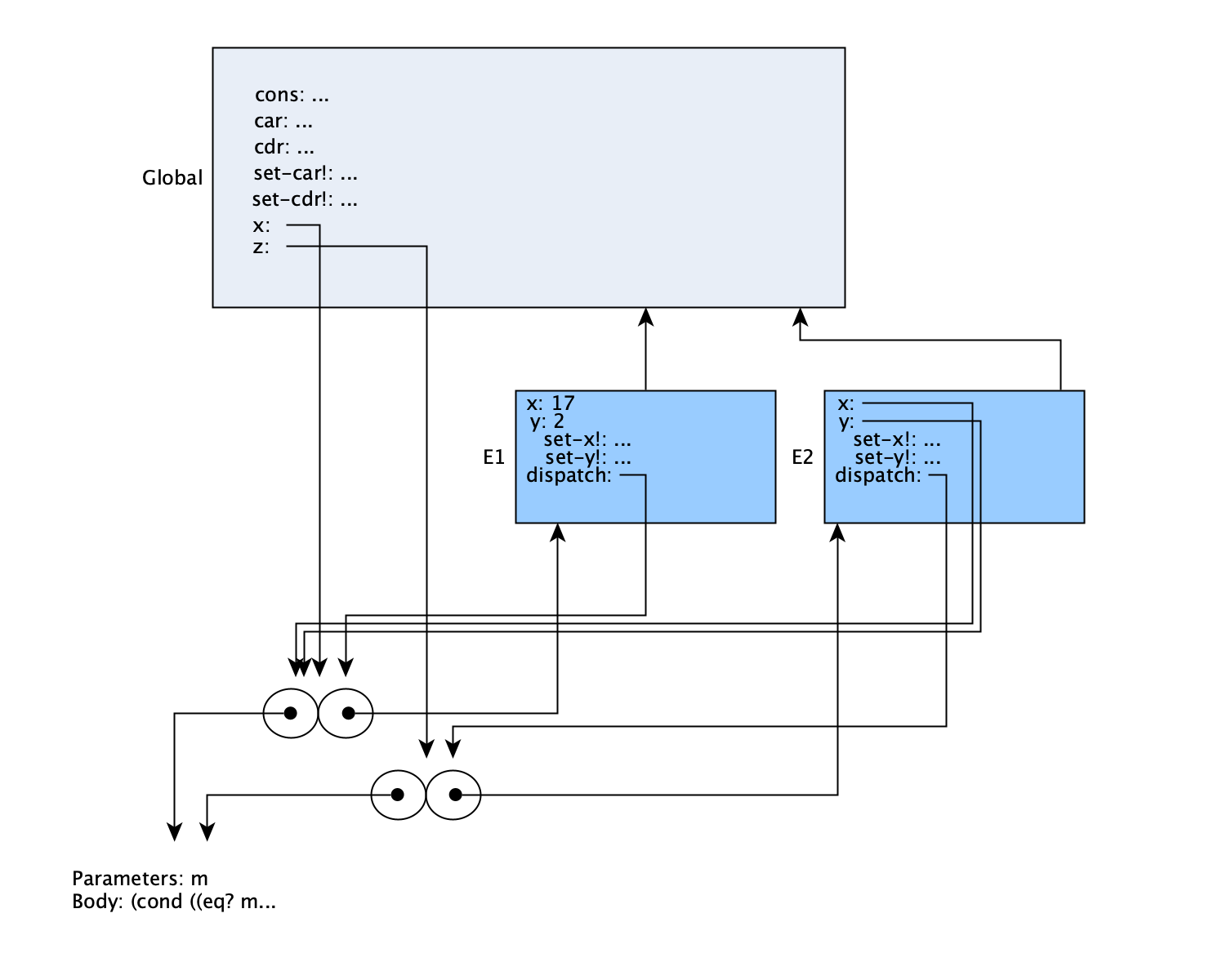
At the end of the call, we can see that this looks essentially the same as the second diagram above, right after global z was created. The only difference is that x in E1 now equals 17. Despite the convoluted approach, what has happened is what we would expect — the value representing the ‘left side’ (car) of the pair x, which was the ‘right side’ (cdr) of the pair z, has been set to the new value.

(car x)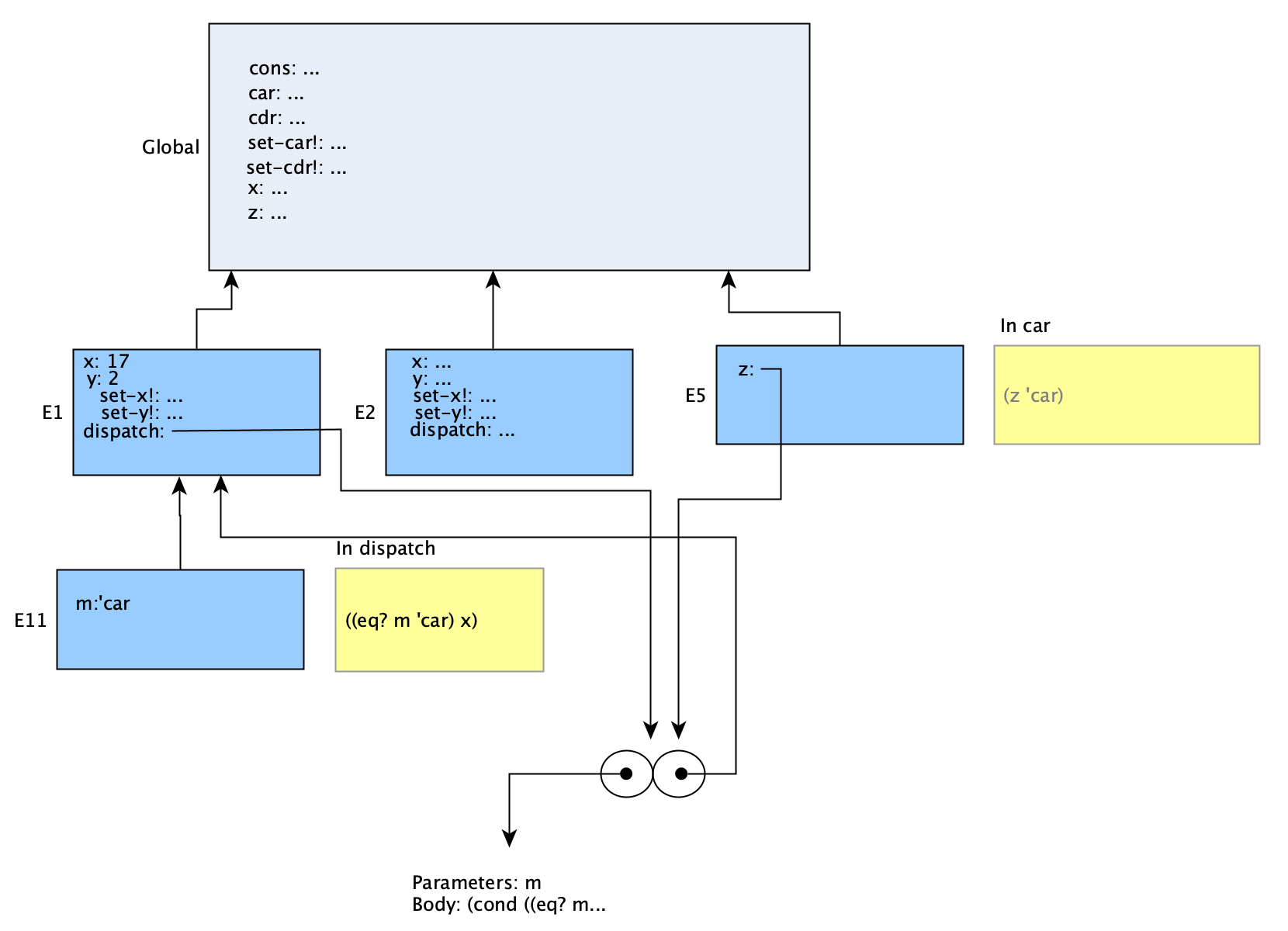

Again, the result of this call just verifies what we expect to be the case. We’ll suffer through the confusing names again, though, just to see how this call plays out. The procedure car uses evaluation frame E5, where z is set to the same procedure as global x. That procedure will be called with an argument 'car, and a new frame E11 is created to evaluate it. When it runs, the procedure matches the argument (in the cond statement) and returns what x is defined as in its environment. Again, E11 lacks a definition for x; it must step back to E1 to find x, defined there as 17. That will then be the result of the dispatch call, which is passed back to car and finally to the interpreter.