Ex. 3.24

Since we are just replacing the equal? call in assoc with our own test, the natural solution is to write a new version of assoc that does that.

(define (assoc-with-test key records equality-test)
  (cond ((null? records) #f)
        ((equality-test key (caar records)) (car records))
        (else (assoc-with-test key (cdr records) equality-test))
        )
  )

The only thing that’s changed is that the equality test needs to be supplied as an argument. The dispatch version of make-table also needs to have a new argument, the test. All calls to assoc have to be updated with the new assoc-with-test procedure as well. Other than that, there are no other changes. Note that the test procedure does not have to be ‘stored’ with the table (e.g. in a separate variable). Since we’re using the dispatch method, the test procedure is preserved in the environment created when make-table was called with that argument.

As an additional note, modern Scheme (R7RS) has a built-in version of assoc that actually accepts a test as an optional argument. If you are working with an interpreter that’s compliant with it, the only change needed is adding the argument.

Ex. 3.25

There are various ways to solve this problem, since the specifications are a bit open-ended. The approach hinted at (following the pattern of the two-key table in the text) would involve storing entire subtables under the keys that need them. A simpler alternative is to just store the entire key list as the actual ‘key’ for the entry, making the whole table ‘flat’ (having only one level). Then the procedures really don’t need to be changed from a single-key table.

After an initial attempt at using subtables, I switched to the flat approach, as it has some advantages in the arbitrariness of the key storage. I also allowed the key list to be unordered. To do this, I needed a procedure that compares lists to see if all items in them match.

(define (all-match? l1 l2)
  (cond
    ((and (null? l1) (null? l2)) #t)  ; both exhausted
    ((or (null? l1) (null? l2)) #f)   ; only one is empty
    ((memq (car l1) l2) (all-match? (cdr l1) (remove (car l1) l2)))
    (else #f)
    )
  )

This checks if the first item in list 1 is somewhere in list 2; if it is, it removes the item from both lists and recurses with the reduced lists. This requires a remove procedure for lists, which returns a filtered list with all items equal to the element removed. These procedures ignore duplicate entries; whether this is a problem or not may depend on whether the key list should actually be hierarchical instead of arbitrarily ordered.

The testing I included checks that items can be placed at any point in the table, and also checks that requests will properly yield the correct result (when the entry does, or doesn’t, exist). There are some optional tests that are more applicable to my approach. Since I can allow the keys in any order, that gets tested. Another optional part is whether a shorter key list overrides a longer one (or vice versa). That would be a concern with the subtable approach, since we’d either only allow one or the other, or need some logic to check whether a key list leads to a subtable or the ‘bare entry’ for that key.

While this makes for a simple implementation, there are potential drawbacks here. As more and more entries are added, it will take longer and longer to locate an item in the table. Potentially every single item needs to be checked to see if it’s a match. It also means storing the entire key list for each item in addition to the item. The subtable approach would split the organization so that less overall space is required, and might cut down on the time necessary to search for it. On the other hand, the added complexity of the subtables might well reduce efficiency. Much depends on the particular application or data set to be used.

Ex. 3.26

All the table implementations so far have stored the table in the form of a list. The first item in the list is a dummy identifier (*table*), and then the rest of the list is a series of key-value pairs. When looking through such a table, we generally examine (or modify) the cdr of the list containing these pairs in sequence. Even if you used a subtable approach in 3.25, odds are that the subtables themselved were kept in a sequential list.

To store the entries in a tree, I replaced the cdr of the list with a tree structure, and perform all the operations on that tree. We had procedures for working with trees in Section 2.3.3. Back then, we stored a single value at each point in the tree; here we store the key-value pair as the value for the node. Lookup is done by checking the keys, and insertion is accomplished the same way values were added to the tree implementation of ordered sets.

The only missing piece here is how to handle the ordering itself. Since we’d like to allow keys to be more than just numeric values, we follow the example of Exercise 3.24 and perform our comparison with an ordering procedure passed in upon table creation. The ordering procedure takes two arguments and determines which is ‘larger’. Following a longstanding pattern for comparison functions, it should return a positive number if the first is larger, a negative number if the second is larger, and 0 if they are equal. The table then can look up and insert items into the correct location based on whatever ordering is needed for the keys.

Although this exercise did not require an implementation, I did make one, re-using as much code as possible from 2.3.3’s tree procedures. The only modifications needed were to allow the use of the supplied ordering procedure. While this is a working implementation, the trees it makes do have the potential issue of becoming ‘unbalanced’ over time. Fixing that, however, would push the scope of the exercise even farther than I’ve already taken it.

Ex. 3.27

It would help us in understanding the environment diagrams to look first at the environments prior to evaluating the statement. Simply defining a memoized function causes several execution frames to be created by the various lambda expressions involved. Note that in addition to the lambda expressions and procedures, each let statement also creates an anonymous procedure and executes it in a new frame. So the definition of memo-fib leads to this:

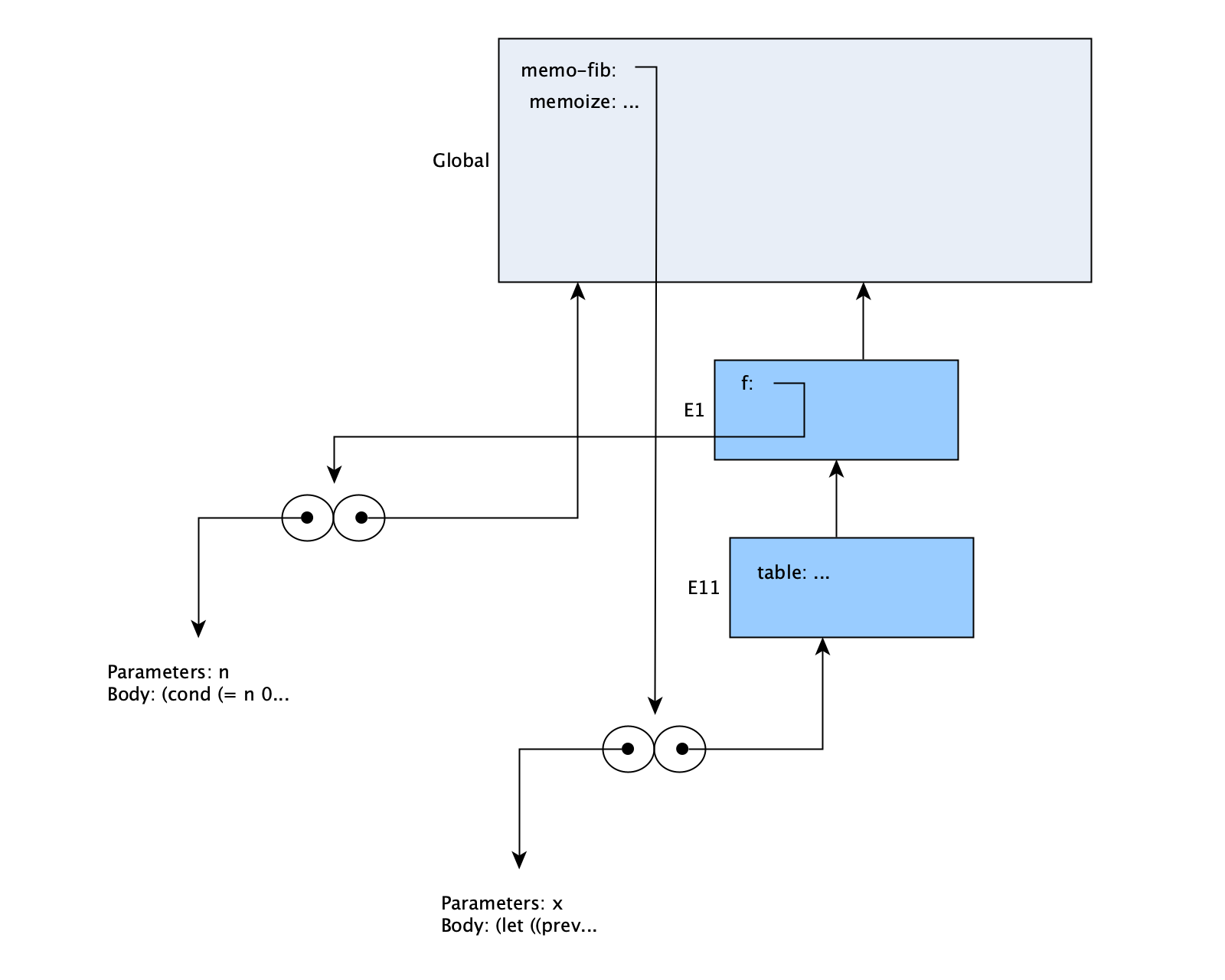
In the definition statement (which is not defining a procedure, and is therefore evaluated immediately) a call is made to memoize, with f set to the lambda procedure that takes an argument n. The table that stores computed values is defined in a let (frame E11), and the value returned by the statement is the lambda with x as the argument (in memoize), and that is what’s assigned to memo-fib.

When we then call (memo-fib 3), we’re passing in 3 as the argument x to that procedure. First, there is a let statement to find previously-computed-result by checking the table. When this returns false, we get another let statement that will assign to result, by calling f to get the value. The procedure f is called with the argument n set to 3, and at that point our environments look like this:

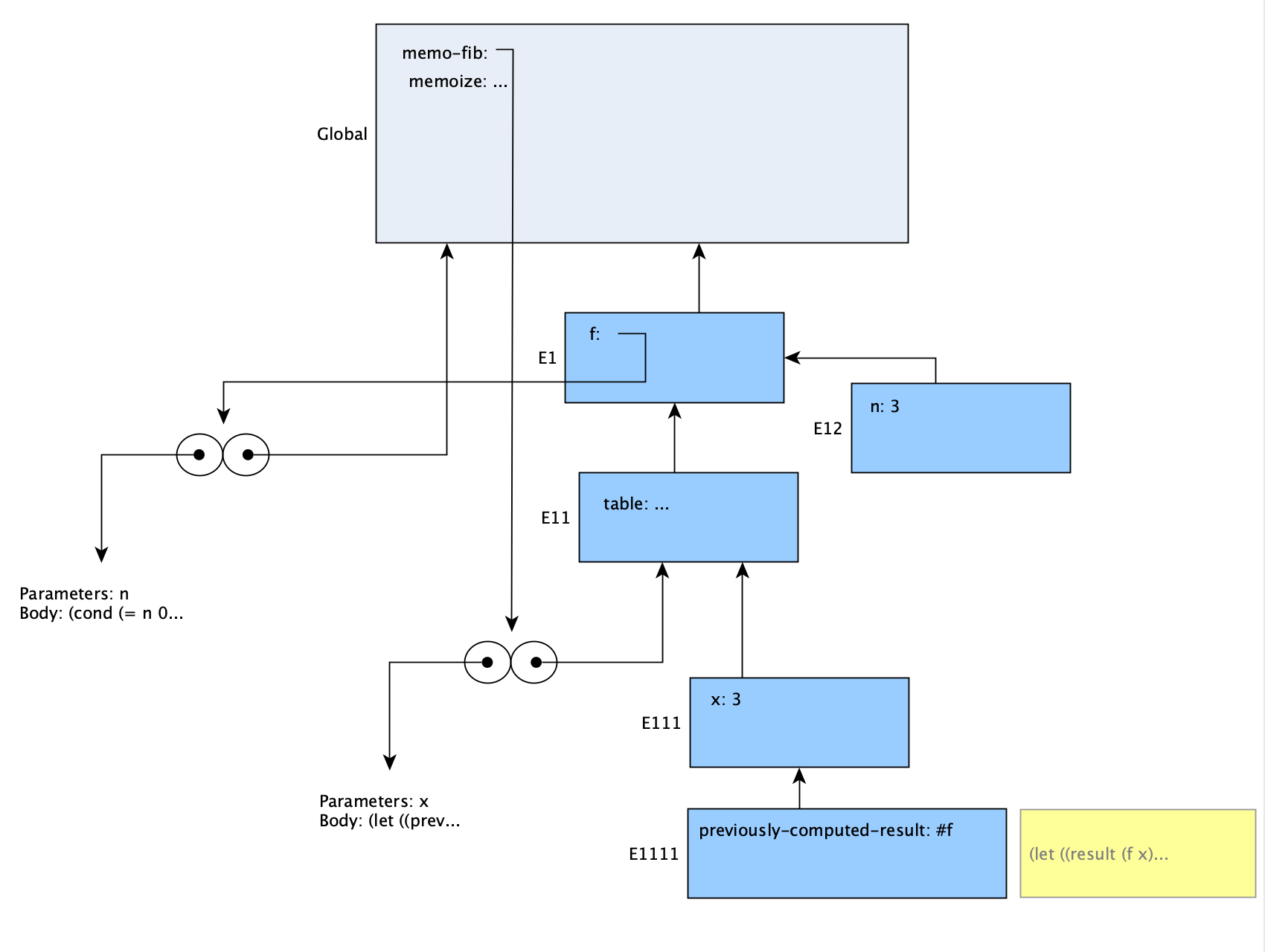
The procedure f will then make a call to memo-fib (the same globally defined function), and since this is the first time it is run, all checks of the table will be false, leading to f being called again with n reduced. In the next diagram we assume left-to-right argument evaluation; either way we’ll reach a point at which f no longer ‘recurses’ into memo-fib.

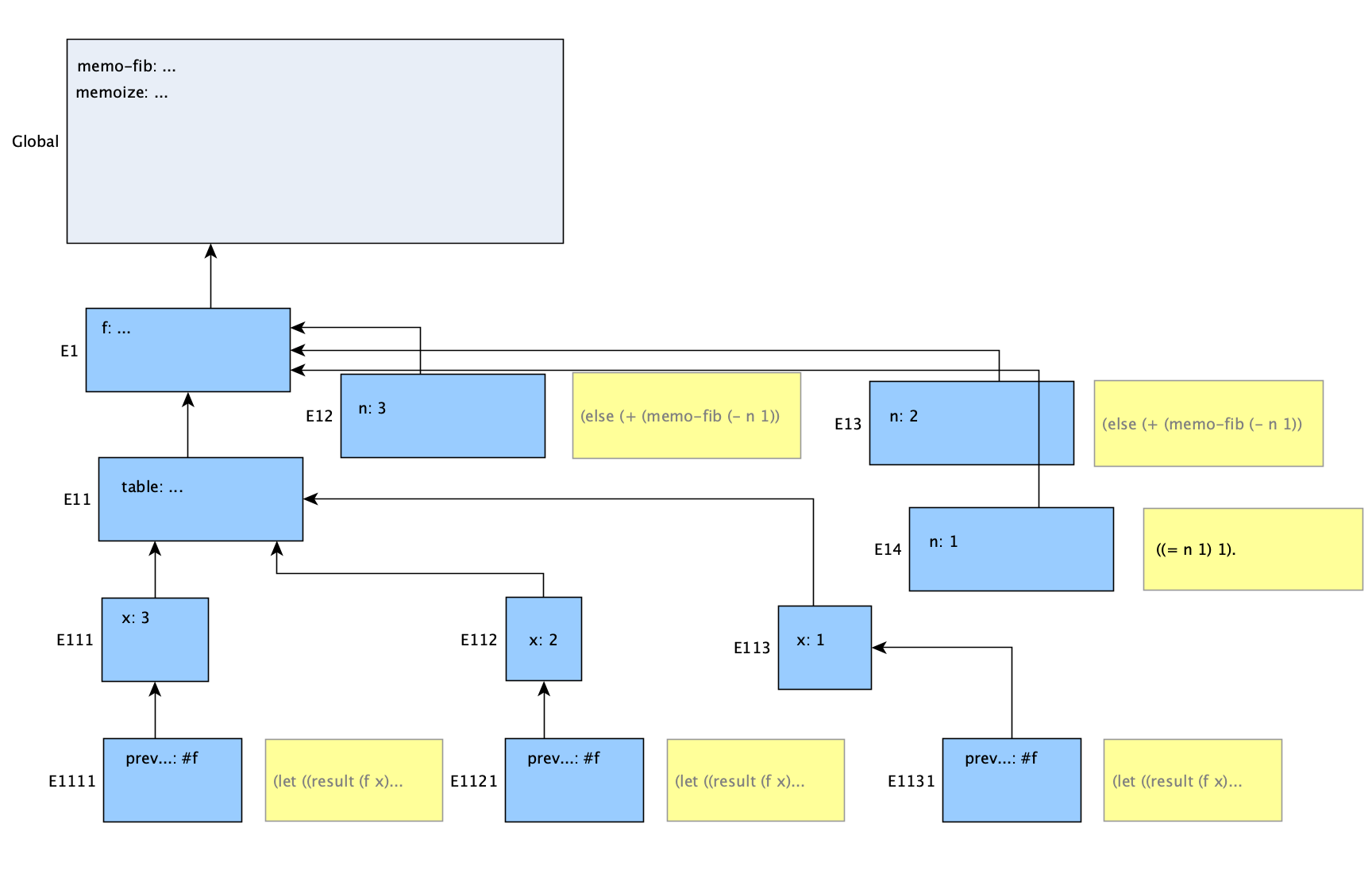
Now, every time we get a final result from those calls to f, it will be stored in the table (referenced in E11) before it gets returned. Eventually we get back up to the first call to memo-fib, when n was 3. Then we will call memo-fib with the argument of 1 (n-2). This time, though, checking the table for previous results will return a value. Instead of another call into f, we just use previously-computed-result as seen here:

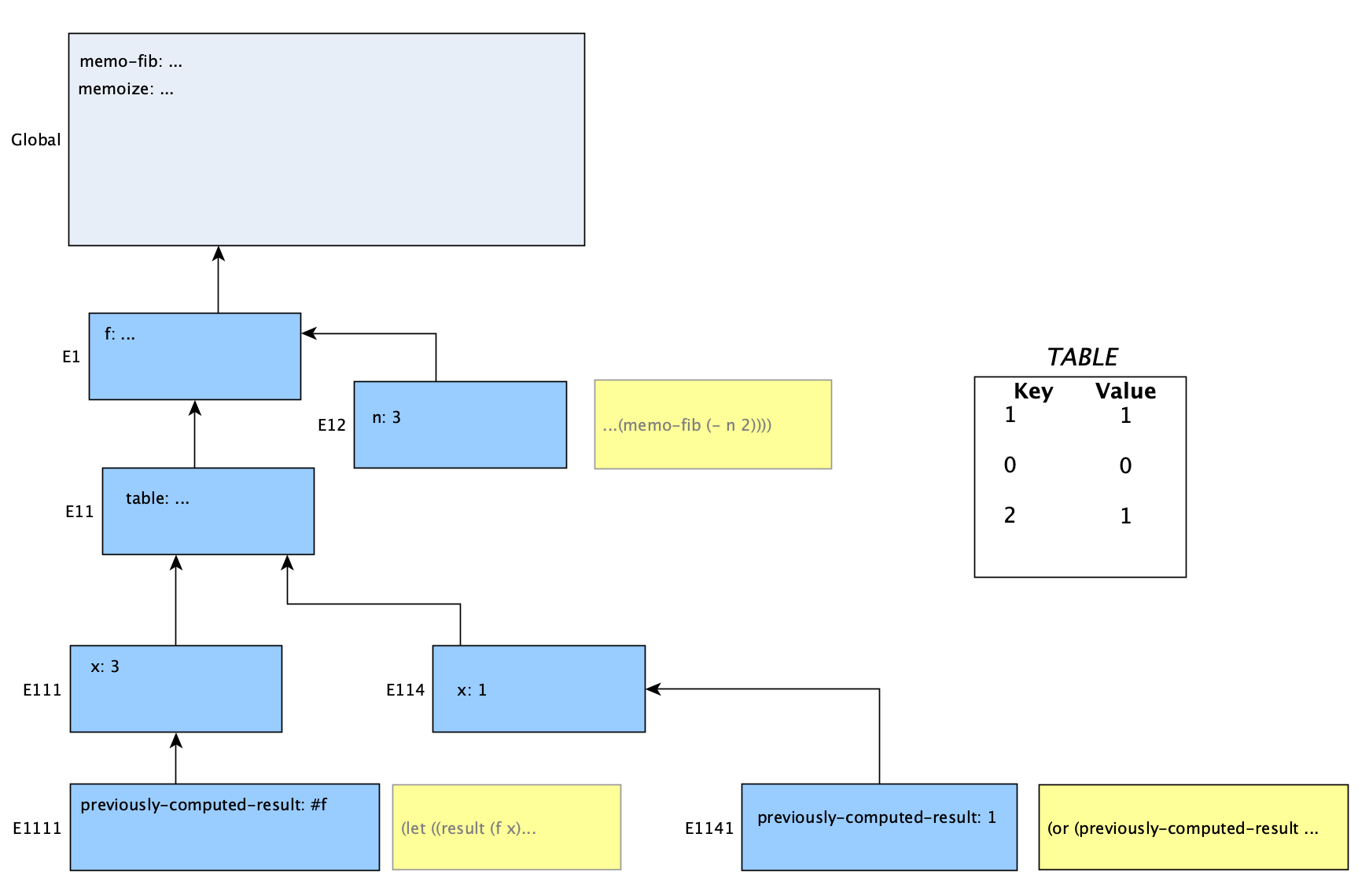
This return value is summed with the return value for n = 2, and the final result of 3 is obtained. Of course it, too, is stored in the table before the procedure returns.

What we see here is that after making calls to compute the most recent Fibonacci number in the sequence, the other one we need (the second-most recent) was already computed and stored in the table. It doesn’t need to be recalculated, just retrieved. In this case, we didn’t save all that much time since 1 is a terminal case, but it should be clear that with higher values, a lot of steps will be saved. Even if the evaluation order was reversed (so that we calculated F(n-2) first), we’d still be saving steps, since to get F(n-1) would only need one more addition. It’d turn out to be the same number of steps required (or saved) either way.

How do we know that the number of steps taken is proportional to n? It should be clear that any recursive call to memo-fib requiring ‘calculation’ steps will only be made once, since after that the time taken will only be that needed to retrieve values from the table. Looking at the process a bit more formally, the total steps required are those needed to compute F(n – 2), the steps to compute F(n – 1), and the steps to sum them. Whichever side we choose to do first, the other value will simply come from the table to be summed. We’ll require n – 1 recursions to ‘calculate’ the value the first time (either directly if it is 0 or 1, or via summing). We can say that as long as table operations are constant, Not just constant lookup but insertion as well calculating F(n) will only require n – 1 recursive ‘calculation’ calls, and n – 2 table lookups. That makes the steps required for the whole process proportional to n.

By running the routine against a timing mechanism (I used Racket’s time procedure) we can verify that this indeed yields a practical improvement in the time taken. However, there was a big assumption we just made above, and it reveals a flaw. It was assumed that the memoization overhead itself (accessing the table) does not add significantly to the steps required in time. Is that really the case, however?

Let’s start with lookup. In a generic sense, any random table lookup must search through the list in order, so we can expect (on average) n / 2 list entries needing to be checked to find the one we want. In memo-fib, the values being looked up are not really random; they are needed in an order that corresponds with the way they are added to the table. With insertion at the head of the list, we tend to get the values we actually want sooner (there is a tiny advantage to calculating F(n -1) first here). Moreover, insertion is something that takes time too. In fact, since insertion checks for duplicates, it’s guaranteed to spend as many equality comparison steps for every insertion as there are entries in the table, since memoization means we’ll never be trying to insert the same value twice! The use of tables for memoization certainly doesn’t come for free.

The reason we did see signficant time savings is that even if it’s not strictly proportional to n, the memoized process is still a more efficient one. This may not have been the lesson intended by the authors, but it is a good illustration of the differences in practical time complexity, theoretical time complexity, and the necessity of understanding the trade-offs that memoization provides. There is a good discussion of this issue (along with a possible fix) at Stack Overflow.

Finally, let’s answer the other question in the exercise. If we had instead defined memo-fib to simply memoize fib, this would not improve the number of steps required for calculation. Since fib makes recursive calls only to itself, none of the values get stored in the table during the computation of the values F(n-1) and F(n-2). The savings in the properly memoized version happens because each time we call memo-fib, it’s an indirect recursion, during which the results are stored and thus available to the other calls to memo-fib that will be made during the calculation. Mere memoization of the function would save time in future calls to memo-fib, but not in the course of a single call to it, since the memoized value is not stored until the call to fib is complete. What we can take from this is that if a function is recursive, the memoized version is the one that needs to be called when recursing, or else the time savings is only on future runs of the ‘top-level’ version of the function.

Solutions 3.3.3