Ex 3.39

First off, we can see that this is similar to the fully serialized approach, and does not affect the situation where one process executes in its entirety before the second one. That gives the result of either 101 or 121 to begin with. We then have to consider how the processes can interleave. The set! step in the first process (P1) is not serialized with the squaring computation. If the squaring is done, and then the second process (P2) happens, and then P1 sets the value, the result of P2 is ignored and at the end x will be set to simply 100. The second process is fully serialized, but since the setting of x in the first process happens with no serializer whatsoever, it could happen at any time, even in the middle of P2. Serializing does not somehow guarantee that the resource is protected from access; it only is protected from access via the serializer. In this case, P2 could read x as 10, then P1 sets x, and then P2 finishes setting x to 11. So four outcomes are still available: 11, 100, 101, and 121. The only possibility that this eliminates is 110, as the reading of x in P1 is certain to be consistent, and will not affect P2.

Ex 3.40

Without serialization, the operations that can interleave meaningfully are the reading of the current value of x and the setting of x. Each appearance of the value x is thus a distinct point where the outcome might vary, although it is only the setting steps that will produce new results. The number of distinct results can be narrowed down to those that occur with no interleaving in the middle, and those that do interleave, in which x changes after one of the times it is read. Those cases can be worked out by hand. Since I had written the interleaving enumeration procedure for 3.4.1, I used it to produce all of them. The results cover the powers of 10 from 100 up to 1000000.

If serialization is used, the ‘middle’ interleaving results are eliminated, while the other results remain. Either they complete in the order listed (squaring first, then cubing), or the cubing occurs before the squaring. But this leads to the same result, 1000000, simply demonstrating that (10²)³ = (10³)².

Ex. 3.41

To see if the balance needs to be protected during reads, we have to consider whether reading it will ever give an invalid result. That would only happen if the balance is changed to anything other than the final result of a given transaction. A withdrawal is the only operation that sets it to a new value, and it only sets it once. Any read will either happen before the set operation or after. Even if we are doing this ‘during’ the withdrawal, it still does not affect the ‘truth’ of our read; we are getting a balance that is correct at some point in time.

There is a hitch in this explanation, though, which leads to an answer for the second question about when this could be a concern. It assumes that the set! procedure is itself an atomic operation. In most circumstances in a computer, and so for just about any practical implementation of this procedure, that is the case. You cannot (from a Scheme interpreter) read a numeric value stored in computer memory while the bits in that value are changing. However, if we consider this in the broader sense of thinking about concurrency, we should keep the idea of atomicity in mind. If instead of a simple number value, the shared resource were some much larger file, or a set of values stored in a table, then it might actually be possible for there to be a hidden intermediate state, in which the data being read is still in the process of being changed and should not be accessed.

Ex. 3.42

The serializer, by definition, only allows one of the procedures in its set to be run at any given time. Whether there are multiple serialized procedures or only two, it doesn’t really matter for concurrency, since there is still only one that can run at a time. In theory, the overhead of having more serialized procedures, if not handled properly in memory, could slow computation down. As a practical matter, it would probably not make a real difference (not that it should be avoided because of that; it seems to be a good change).

Ex. 3.43

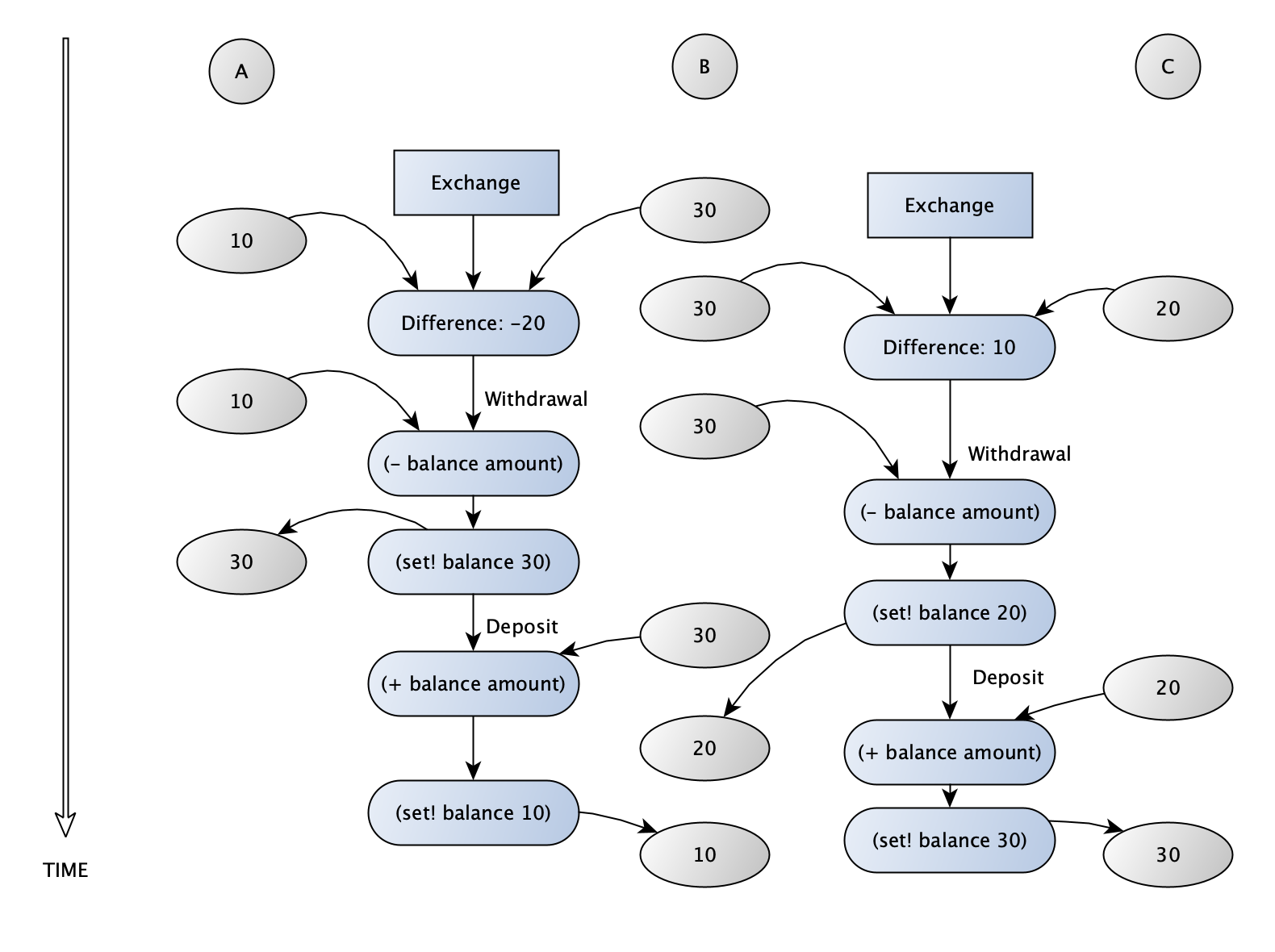
Let’s label any two existing account balances as X and Y. With the exchanges fully serialized, then whenever one happens, the difference between them D (equal to X – Y) is computed. That amount D is withdrawn from the first account. Since the exchange is serialized, the first account must still have a balance of X at the start of the withdrawal, and the result of the withdrawal gives it a balance X – D, which is equal to Y . Next, the amount D is deposited to the second account, which similarly cannot have changed, and its balance becomes Y + D, which is equal to X. Neither account can be externally modified during the time when the difference is calculated and the withdrawals and deposits occur. If many exchanges are made, we cannot predict in the end where a given amount will end up, but we know that X and Y must be present somewhere as a result of these calculations; this extends to any other initial account balances that we include in the exchange sequence.

If the serializers are only on a per-account basis, that means the account balances can change after the difference is computed, since the access to determine the difference is separate from the deposit or withdrawal. In that case, removing the past difference from one and adding it to the other will not necessarily result in their values being exchanged. We do guarantee that the difference removed will be faithfully recorded in the balance of the first account, and just as properly recorded when added to the balance of the second account. That’s how we can say that the total amount of money in all the accounts does not change.

There would be trouble if withdrawing a given difference incorrectly hits the ‘insufficient funds’ error. The assumption for this exercise is that this is avoided, or that account balances are allowed to be negative when considering the ‘sum of the balances’.

Here’s the sequence of transactions (note that negative-valued ‘withdrawals/deposits’ are occurring):

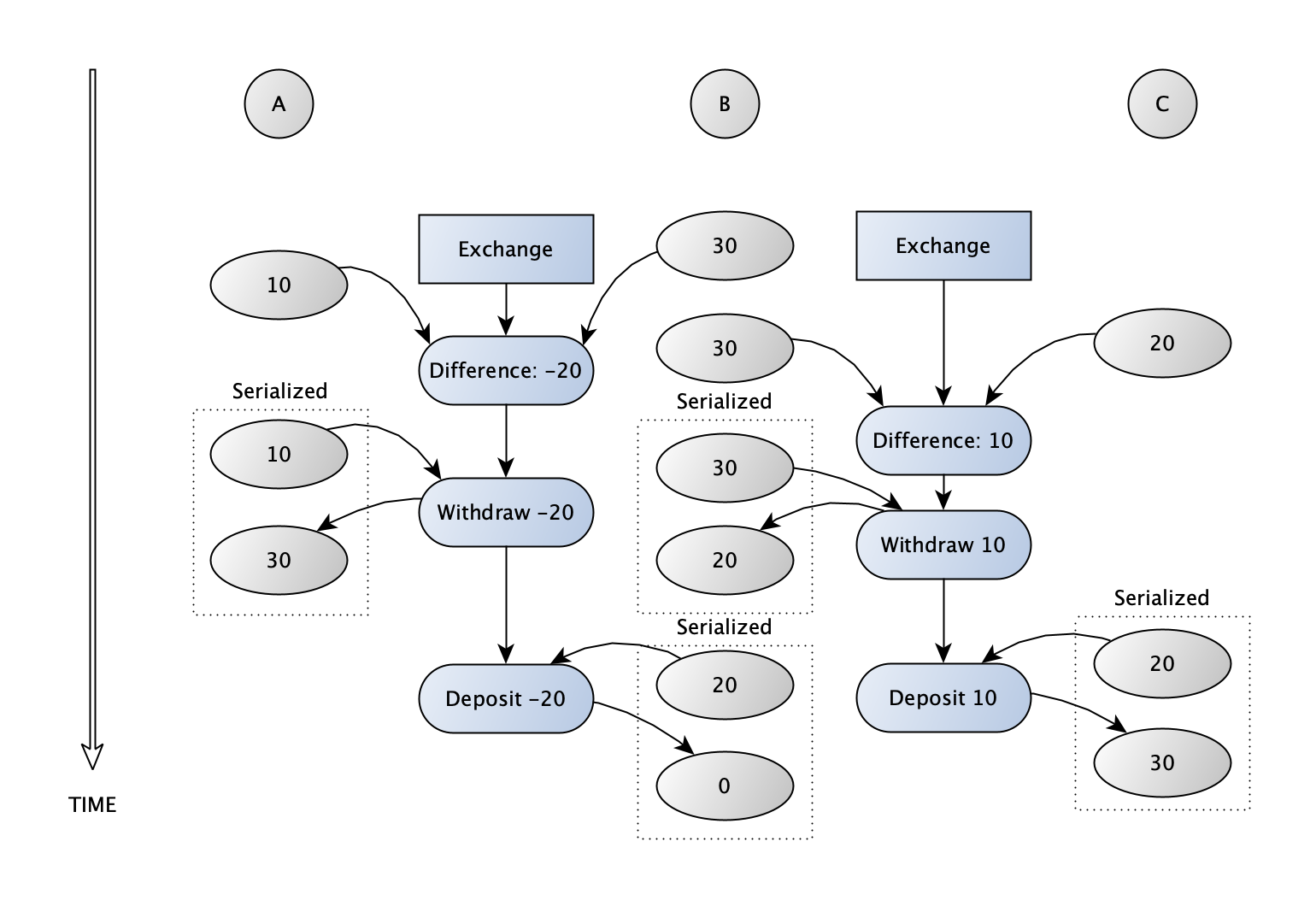
In the last case, if there is no serialization on the accounts, then it is all too easy for one transaction to overwrite the effects of another. A withdrawal can happen during a deposit, causing the balance to be set to what it would be had the withdrawal never occurred. In this case, although the difference is added to the second account, it may not have been properly removed from the first account. We would effectively double the difference and that money could appear in both accounts. This could also go the other way, causing the difference to be withdrawn from the first account but not properly added to the second, resulting in it being ‘lost’. The diagram below shows the first situation. The withdrawal from B is not properly recorded, so that the total amount of money in all three accounts ends up increasing.

Ex. 3.44

The transfer does not require the same sort of guard against errors that swapping did. Each account is only accessed once in the course of the transfer, and the transaction with one account does not rely on the balance in the other account. There is therefore no problem that requires serializing the accounts in conjunction with each other. In the exchange, both account balances were first accessed to calculate the difference, and each account was later used with the expectation that the balances had not changed in the meantime.

Ex. 3.45

The central problem here is that if external procedures are using the same serializer, you’d have multiple procedures in the same serialized set. If any procedure already has control of the account’s serializer, it cannot then call the withdrawal or deposit routines, because those would be waiting on the same serializer to be released. This would result in the program locking up.

The difficulty of deciding who is allowed control in this sort of ‘token-based’ concurrency scheme is one of the thornier issues to be dealt with. If it’s managed tightly and automatically, that can limit the power and extensibility of the system. If it is left more open, however, a greater burden is placed on the users of the system, and a greater potential for misuse is present as well.

Ex. 3.46

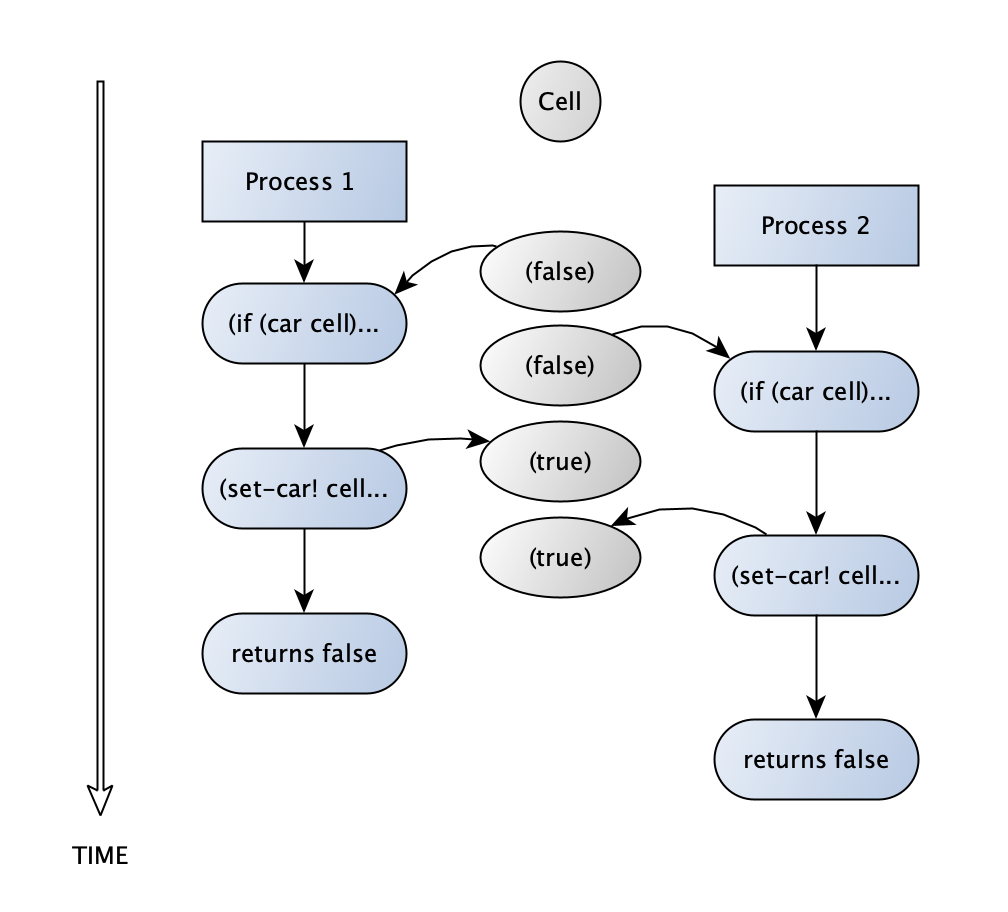
If the testing and setting are not accomplished without interruption between them, it’s entirely possible for two concurrent processes to interleave the read and set steps within the test-and-set! procedure. That results in two processes that both read a ‘clear’ value for the cell (i.e. false), and then go on to set it. Both then continue as if the resource is available to only them, when in fact they are potentially accessing it at the same time.

Ex. 3.47

The mutex approach uses a single mutex to protect the count of currently available accessors, stored as a numeric variable. If we get an acquire request and the count is higher than 0, the number is reduced and access is granted. Otherwise, we keep retrying until the number comes back as more than zero and we can proceed.

(define (retry)
    (sem-mutex 'release)
    (sleep 0.1)
    (the-semaphore 'acquire)
  )

(define (the-semaphore msg)
  (cond ((eq? msg 'acquire)
         (sem-mutex 'acquire)
         (if (= 0 free-count)
             (retry)
             (set! free-count (- free-count 1))
             )
         (sem-mutex 'release)
         ) 
        ((eq? msg 'release) 
         (sem-mutex 'acquire)
         (if (< free-count n)
             (set! free-count (+ free-count 1))
             )
         (sem-mutex 'release)
         )
        (else
         (error "Undefined operation for semaphore : " msg)
         )
        )
  )

Using test-and-set!, I went with the approach of using multiple cells to store the current state of accessors, without any particular indication of which process sets which cell. The trickiest part of doing it this way is figuring out how to check for an available cell in the list either while acquiring or releasing. I stored the cells in a ‘ring’, which is to say a circular list. When acquiring, we check whatever cell we are at using test-and-set!, and if that one is already set, we continue around the ring. Once a cell is available, we can stop circling and return, since we have now acquired the resource. This replaces the recursive ‘retry’ step of the mutex with simply circling the list. As long as the number of requests is a reasonable ratio to the size of the semaphore, the problem of ‘crowding out’ other requests is likely avoided.

Releasing works in a similar fashion, by grabbing a cell and checking if it is already set, and continuing to check around the ring for a cell that is set (and can thus be cleared). There is a potential pitfall here — the clear! procedure does not care whether the cell is already cleared. This would be a problem if two concurrent releases are clearing the same cell, as only one cell would actually be released. To avoid this, there is a release-lock cell that forces all releases to be sequentially processed (it works essentially as a mutex), so that only one will be clearing a given cell’s contents at a time.

At first glance, this might seem to lead to strange results. One process might go in and set a cell using test-and-set!, and immediately after that another process comes by and clears that same cell! This isn’t actually a problem, however. The cell that a process sets does not have to be the same one it clears. All that really matters is that the total number of set and unset cells is correct. So even if a situation of a cell being set and cleared almost immediately occurs, we can be confident that there is still a cell somewhere that was set by the process that is now releasing a cell, and the number of set or unset cells stays correct.

Here are the two routines for acquiring and releasing the cell list. We can see that the release is reading the cell and then clearing it as two steps, and this makes clear the need for the ‘release-lock’ to wrap the process. An alternative would be an atomic ‘test-and-clear!’ but we do not have that.

(define (acquire-first-available li)
  (if (null? li)
      (error "Circular semaphore ring has terminated list: Cannot continue")
      (if (test-and-set! (car li))
          (acquire-first-available (cdr li))
          true
          )
      )
  )

(define (release-next-available li)
  (if (null? li)
      (error "Circular semaphore ring has terminated list: Cannot continue")
      (if (car (car li))
          (clear! (car li))
          (release-next-available (cdr li))
          )
      )
  )
  

Ex. 3.48

The situation of account exchange works as long as all processes that require multiple accounts proceed in the same order. To simplify things, we’ll just assume we have numbered them Account 0001 and Account 0002. The proposed method prevents any exchange from acquiring access to Account 0002 unless it has already acquired access to Account 0001. Once an exchange has control of Account 0001, no other exchange can begin, since the other exchanges will be waiting on access to Account 0001. That means there can be no deadlock, since no other processs will first acquire Account 0002 and wait on access to Account 0001.

Adding numeric ids to the account is not a difficult task. For the purpose of this exercise I gave them random large numbers. A proper approach would be to use a sequence generator of some sort, with local storage in the ‘generator’ function to ensure that a unique account number is always created.

To modify the serialized exchange, we just check which account is greater, and acquire the lower one first by calling it as the argument of the higher one’s serializer. Note that it doesn’t particularly matter whether we choose the smaller number or the larger one, as long as we are consistent with all procedures that might need to access more than one serializer.

(define (serialized-exchange account1 account2)
  (let ((serializer1 (account1 'serializer))
        (serializer2 (account2 'serializer))
        )
    (if (< (account1 'account-id) (account2 'account-id))
        ((serializer2 (serializer1 exchange)) account1 account2)
        ((serializer1 (serializer2 exchange)) account1 account2)
        )
    )
  )

Ex. 3.49

As explained in the previous solution, this particular deadlock avoidance technique relies on the procedures that are using multiple accounts to always acquire access in a particular order. That implies that not only are all the steps in the procedure already known, but that all the resources that will be needed can also be checked before starting any of the steps, in order to generate a consistent ordering. Of course in many, and probably the majority of situations, the process cannot know all of the steps or resources required until it begins or is partially complete. There could be information stored in one resource that itself determines which resources are needed later. Or the result of an operation must be computed before knowing which step to execute next, meaning that there are multiple ways in which a process can execute a given sequence.

To keep with the bank account example, suppose accounts can have a linked ‘overdrawn backup’ account that will be used in the event that there are insufficient funds in the first account. In order to determine whether the backup account access is needed, the process would have to perform the withdrawal on the first account without interruption, and then gain access to the backup account. If it merely checks for sufficient funds before, another process could reduce the account balance in between; the whole process must be serialized. But if an exchange was occurring between an account and one that was linked as its backup account (and the backup had a lower account number), the process would result in a deadlock, since access to the backup account would already have been granted when the exchange began.

While it would be possible to deal with that specific case by establishing various rules, the issue being raised here is that altering the features of a system that relies on a specific method for deadlock avoidance will likely cause these complications to arise. That emphasizes the necessity of taking special care when dealing with concurrent systems, as most of the time we make assumptions about the consistent state of the underlying system, and when it could change at any time, it is much harder to write code that can account for all potentialities.

Exercises 3.4.2.